TACOM HQ™
Command Results
CAGE 834B9 SAM GHMFLBP9GGM3
“Incoming fire has the right of way." - Unknown
Structured Barrel®
INTEL
• Large diameter, ultra-rigid harmonically quiet barrels.
• Advantages
– Reduced deflection
– Temperature resistance
– Flatter SD
– Less mirage
– Minimal load development
– Improved life
• Patented barrel technology
The following offers various physics and mathematical proofs peer-reviewed by multiple aeronautical engineers as well as FEA (Finite Element Analysis) simulations using MSC/NASTRAN and LS-DYNA to exhibit the superiority of Structured Barrels:
UNDERSTANDING BARREL FLEXION AS WAVES
Axial Stiffness
Structural stiffness is a measure of an object’s resistance to deflection when subjected to a force, and axial stiffness is one form of measurement. Axial stiffness refers to a structure’s resistance to deformation along the object’s longitudinal axis when a parallel force is applied, and is quantified by a coefficient that represents the relationship between axial force and the resulting axial displacement ie elongation.
One of the most basic examples, in finite terms, is an axial spring. The equation for deflection known as Hooke’s Law and is given by the following equation: F = kx, where F is the applied force, k is the spring stiffness constant / coefficient, and x is the displacement. The following image demonstrates as load increases, deflection increases. Less visually obvious, though, is the relationship that as the spring stiffness increases, the deflection decreases, In a rifle barrel, the axial stiffness is a linear function of the cross-sectional area and the modulus of elasticity of the material.
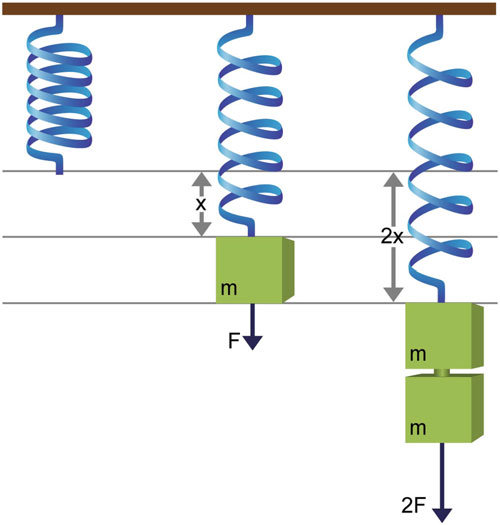
Common applications and analyses for Axial Stiffness involve structural engineering where evaluating a system’s stability and load bearing capacity influences factors like deflection and resistance to axial loads. This includes structural weight, external forces, and mechanical systems like shafts and columns where axial stiffness determines the structure’s ability to maintain alignment when subjected to axial load. It also includes vibration as this affects how an object elongates and contracts, affecting its overall dynamic behavior.
Bending Stiffness
Similar to Axial Stiffness, Bending Stiffness is the measure of an object’s resistance to deflection when subjected to a lateral load, or end bending moment. This concept is easily simplified by evaluating a beam in the below figure. As we can see by increasing material distribution in the plane of an applied force yields greater resistance to bending. Click here for a video animation.

Deflection under bending loads may be calculated using closed form equations for simple cross-sections, but for variable section beams, like Structured Barrels, a more complex method such as finite elements is required. In general, however, Bending Stiffness is linearly related to the moment of inertia of the cross-sectional area, Ixx. In other words, the relative bend resistance for two objects (standard versus a Structured Barrel) can be estimated by comparing their respective moments of inertia. Using this parameter allows one to determine the section stiffness as a function of section area.
Harmonics
Structural stiffness, material stiffness (modulus of elasticity), and mass distribution are all functions that determine an object’s harmonic mode as all objects exhibit a natural frequency. When subjected to an impulse load, wave functions that originate from within an object propagate at this natural, fundamental frequency. In other words, changing an object’s structural stiffness (length, diameter, Bull and Structured Barrels), material stiffness (metals and alloys), and mass distribution (muzzle brake, suppressor, and tuners) fundamentally drives an object’s resistance to deflection. Each yields varying degrees of influence though depending on the scale of the variable change and its relationship to the system’s overall function.
This concept can be clearly understood by considering the sound an object makes when struck. The pitch of that sound is the audible frequency at which the object is vibrating. For example, when a tuning fork undergoes resonance, it continues to vibrate until energy dissipates through work and friction.
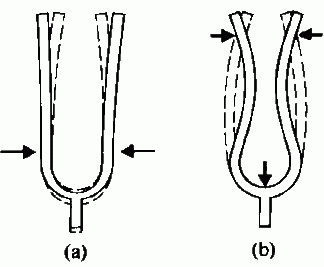
Similarly, barrels vibrate due to load impulses during a firing sequence, as barrels too vibrate at their natural frequencies. In the case of rifles, however, it is not just the barrel stiffness, but the attachment to the stock/chassis, the stiffness of the bipod/mount, the stiffness of the bipod interface with the ground, and also the stiffness of the rifle interface with the shooter. Each of these interfaces are essentially springs of varying stiffness that affect the overall dynamics of the system.
Wave functions that diverge from an object’s fundamental frequency generate irregularities and non-repeating wave patterns that induce amplitudes perceived as vibration. Vibration propagates with ideal efficiency through uniform, homogeneous objects and mediums.
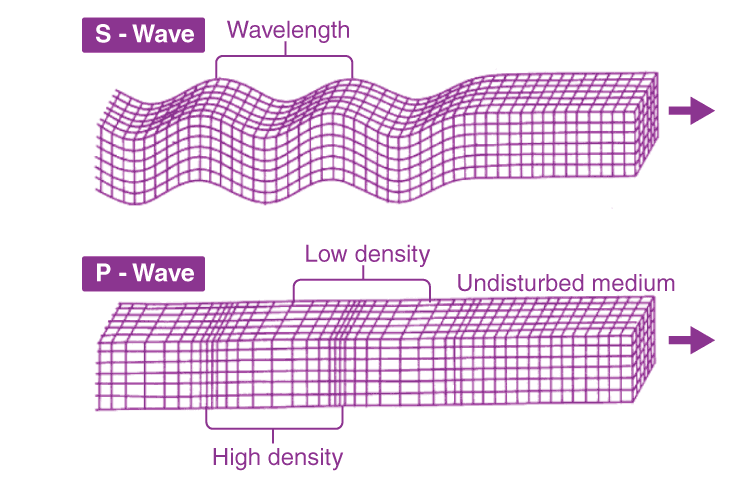
P and S Waves
Harmonics consist of S and P waves. S waves translate sinusoidal functions while P waves are complex sheering functions generated from compressive and expansive forces. When a barrel resonates, S and P waves are propagating through the barrel at 8,000 and 13,000 mph, respectively, traversing the entire barrel many times before the bullet even exits the muzzle. Examples of a S and P waves include barrel whip and the momentary compression of the barrel acted by bullets engaging rifling and high bore pressure, respectively.
Temperature and Waves
The speed with which these functions travel varies by temperature as temperature describes atomic vibration. Greater the temperature yields greater atomic vibration and thus the distance between each atom also increases; increasing the time for one atom to collide with another atom to relay a wave at some frequency. Since all atoms vibrate, a consequence of having a temperature above absolute zero, temperature and atomic vibration determine the four material states: solid, liquid, gas, and or plasma. Since harmonic frequencies travel more efficiently through solids than liquids due to differences in atomic arrangement density with only minor energy loss in the vibration of the atom itself, waves travel faster through solids than liquids and so on, which is described by the following equation λf = v. Click on the following video animations on Sound Waves and Sound Propagation in Different Mediums.

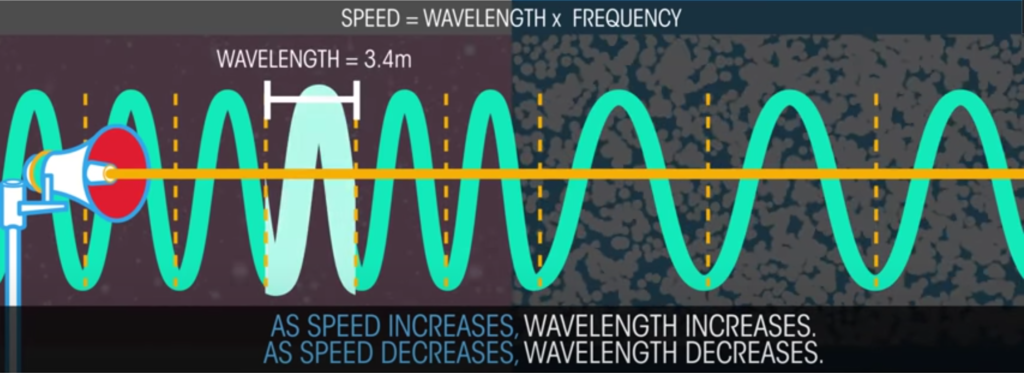
Therefore, as heat flows from high to low energy state(s), from low to high entropy, incremental changes in temperature induce infinitesimally small changes in the efficiency of the medium to conduct wave functions as the medium itself undergoes infinitesimally small material state changes. Changes in barrel temperature – cross section by cross section – cause atoms to undergo infinitesimally small phase shifts from solid to liquid during long shot strings, changing the associated distance between each atom, and thus causing wave functions of varying speeds and wavelengths that generate changing constructive and destructive interference patterns along its entire length and temperature gradients.
Barrel Flexion
Wave functions are a derivative of flexion caused by gas pressure, recoil, gravity (torquing the barrel), rifling, and bore contours that cause bullets to push/pull barrels into new shapes.
Bore contours are common as no bore is absolutely straight. Deep hole drilling yields average tolerances of 0.001-0.003″ per inch, and these contours can be in one or multiple directions and are almost never linear. Thus, the 100’s or 1,000’s of ft-lbs of force imposed by bullet acceleration causes flexion. This push/pull induces a sinusoidal wave that relays the speed and magnitude of the push/pull that ripples along the barrel at a certain frequency. Since these frequencies travel many times faster than the bullet, they create amplitudes that can further exaggerate the bullet’s push/pull on the barrel, causing greater deflection and accelerations about its center axis that is perceptible as barrel whip.
Ladder Tests
A standard barrel’s geometry exudes sufficient axial and bending stiffness; however, like all systems, nothing is absolutely rigid. Energy is lost accelerating the barrel into a dynamic state from gas pressure, recoil, gravity (torquing the barrel), rifling, and bore contours, and this acceleration affects the timing with which the bullet meets an amplitude, causing different compressive and tensive forces (push/pulls).
Applying a metric where 67% and 95% of groups will fall within a 1 and 2 standard deviation, respectively, this is commonly referred to as a Gaussian distribution. Bell curves like this are common to predict the likelihood of specific outcomes in various scientific disciplines. In other words, a rifle that yields a 0.5-moa group will do so most of the time. Appreciating Gaussian distribution, the institution to zero from multiple 5×5 data points, ideally starting from cold bore, aims to average variables that affect internal variable control. It is for this reason ladder tests, where powder charge may be incrementally increased in half grain increments in a series of 5-10 shot groups, can be effective at finding a harmonic node, as it reveals a combination where the overall sinusoidal wave exhibits minimum amplitude (flexion) across x-rounds.
In theory, ladder tests should yield vertical groups with points of impact increasing in relation to increases in velocity if all other variables are kept constant, but ladder tests almost always yield horizontal dispersions. Given rifling only marginally affects BC (1-2% on a “shout-out” barrel) and hand loads further reduce error found in principal axis tilt, pressure curves, etc., stark changes in group size and or position suggest other forces are acting on the system. Shooters can compensate using their scope, zeroing to an observed position of precision. For example, if A-bullet shot an average (x,y) and B-bullet shot (x+1,y+1), technically, one could dial out the “+1” movement and make that zero. However, this zero is now calibrated to those conditions, and changing ambient air temperature or barrel temperature from sun soak or long, shot strings changes a barrel’s harmonic behavior. Thus, barrels that experience horizontal dispersions from small variable changes are reacting to one or more of the causes for barrel flexion, which will only be exacerbated by heat and thermal expansion.
Second Moment of Area
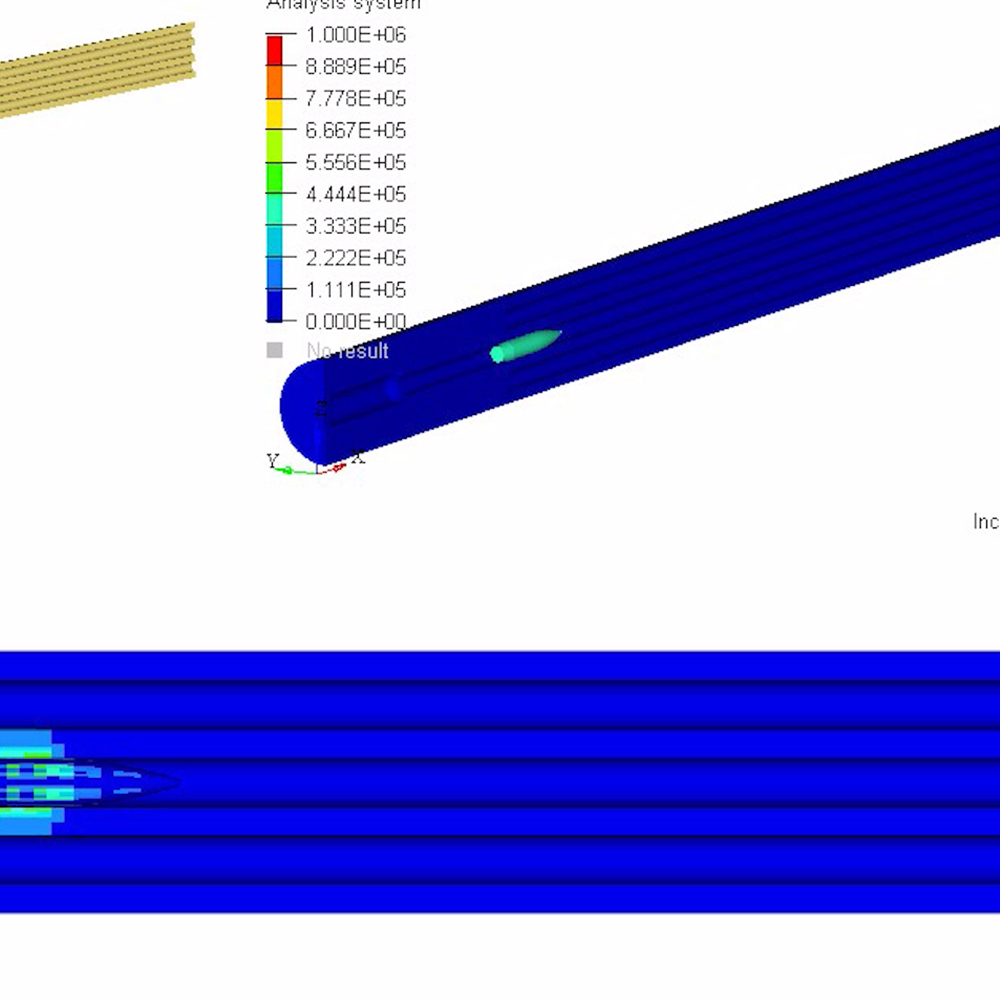
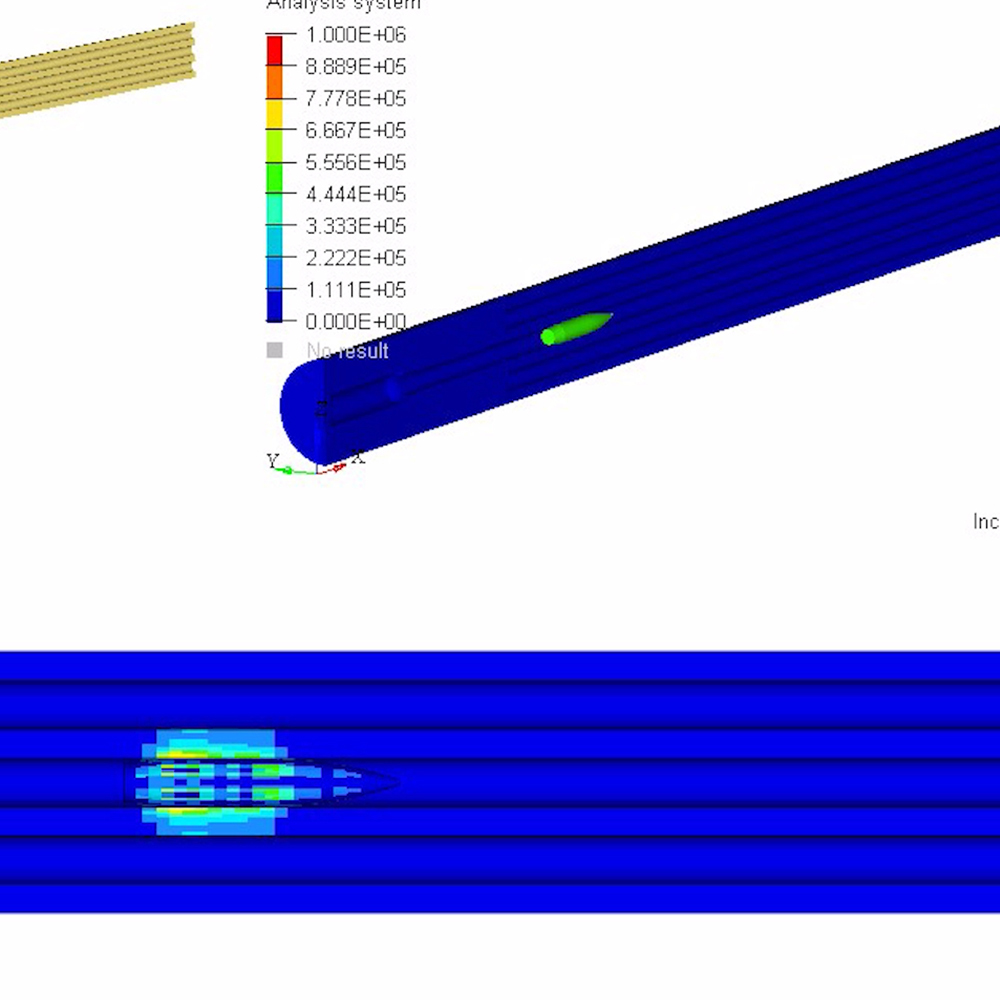
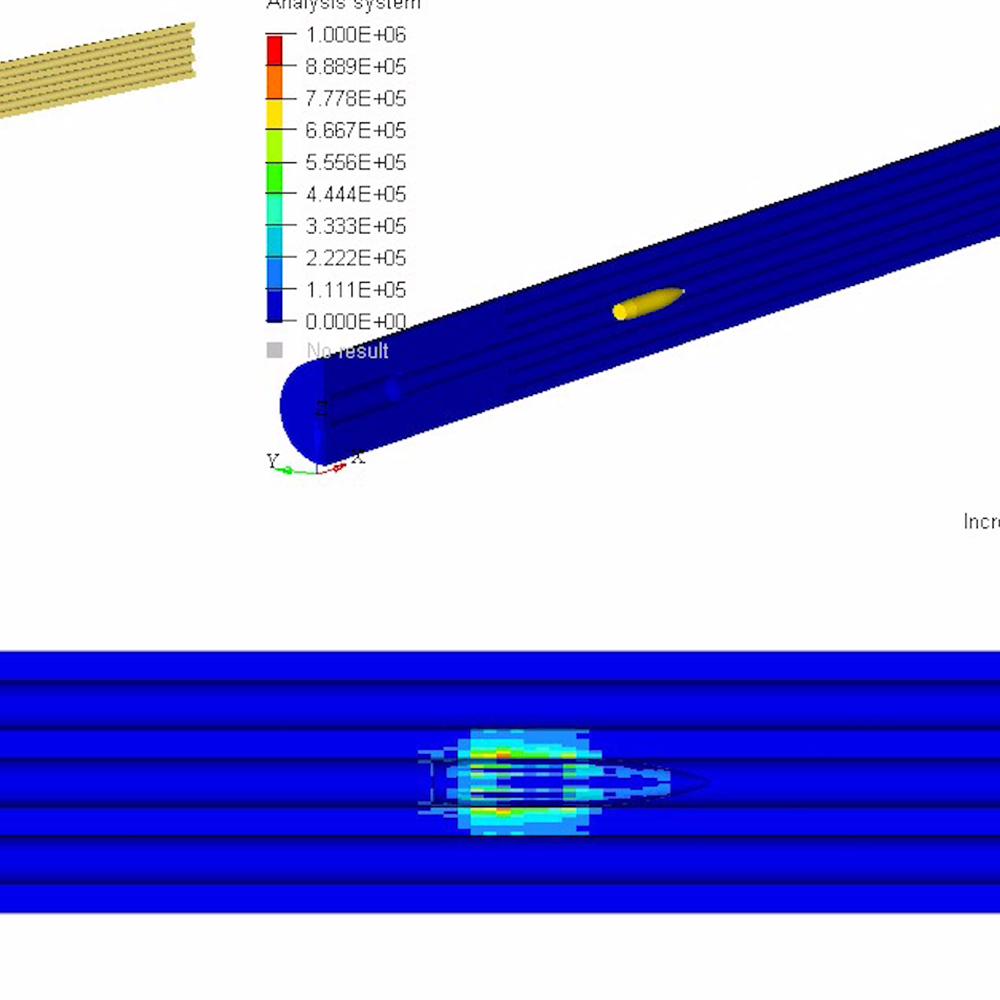
Upon powder detonation and bullet acceleration, the imposed S and P wave functions transfer enormous energy into the compression, tension, and torque of the barrel. As these linear and radial wave functions traverse the barrel, amplitudes manifest as acceleration and thereby induce a velocity. The resulting angular velocity of the barrel about its center axis is described by its moment of inertia while its flexion is described as its second moment of area.
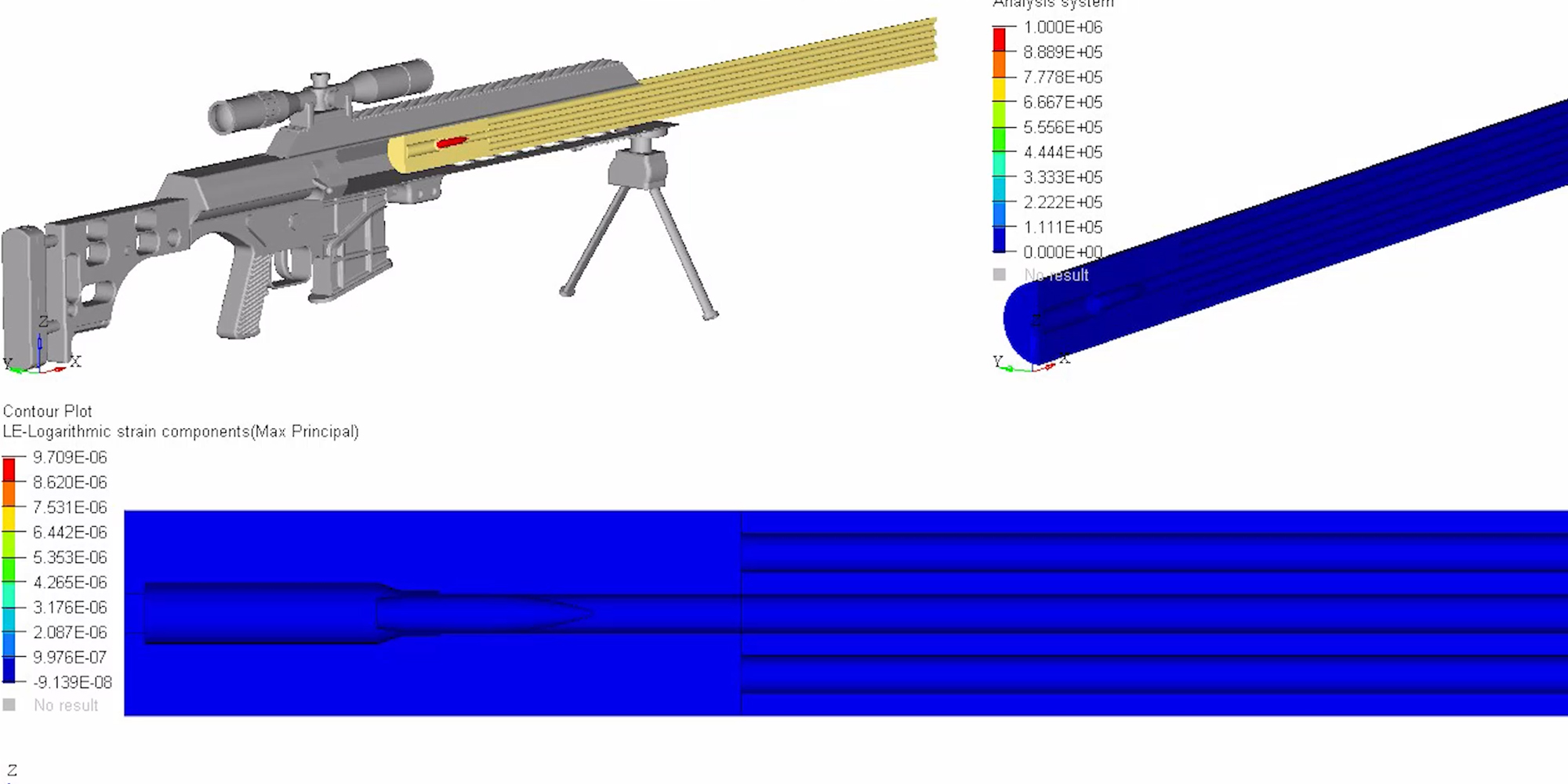
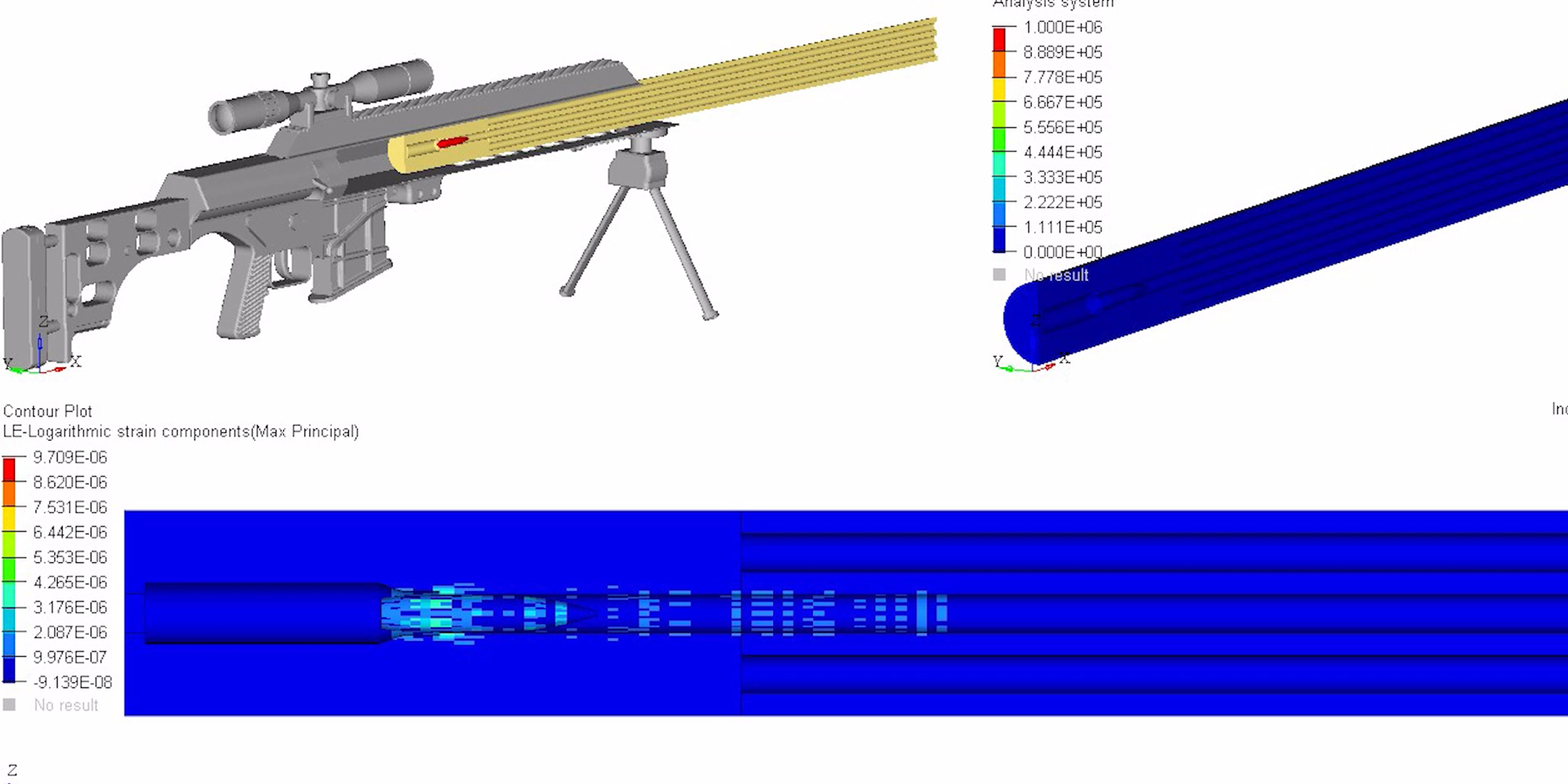
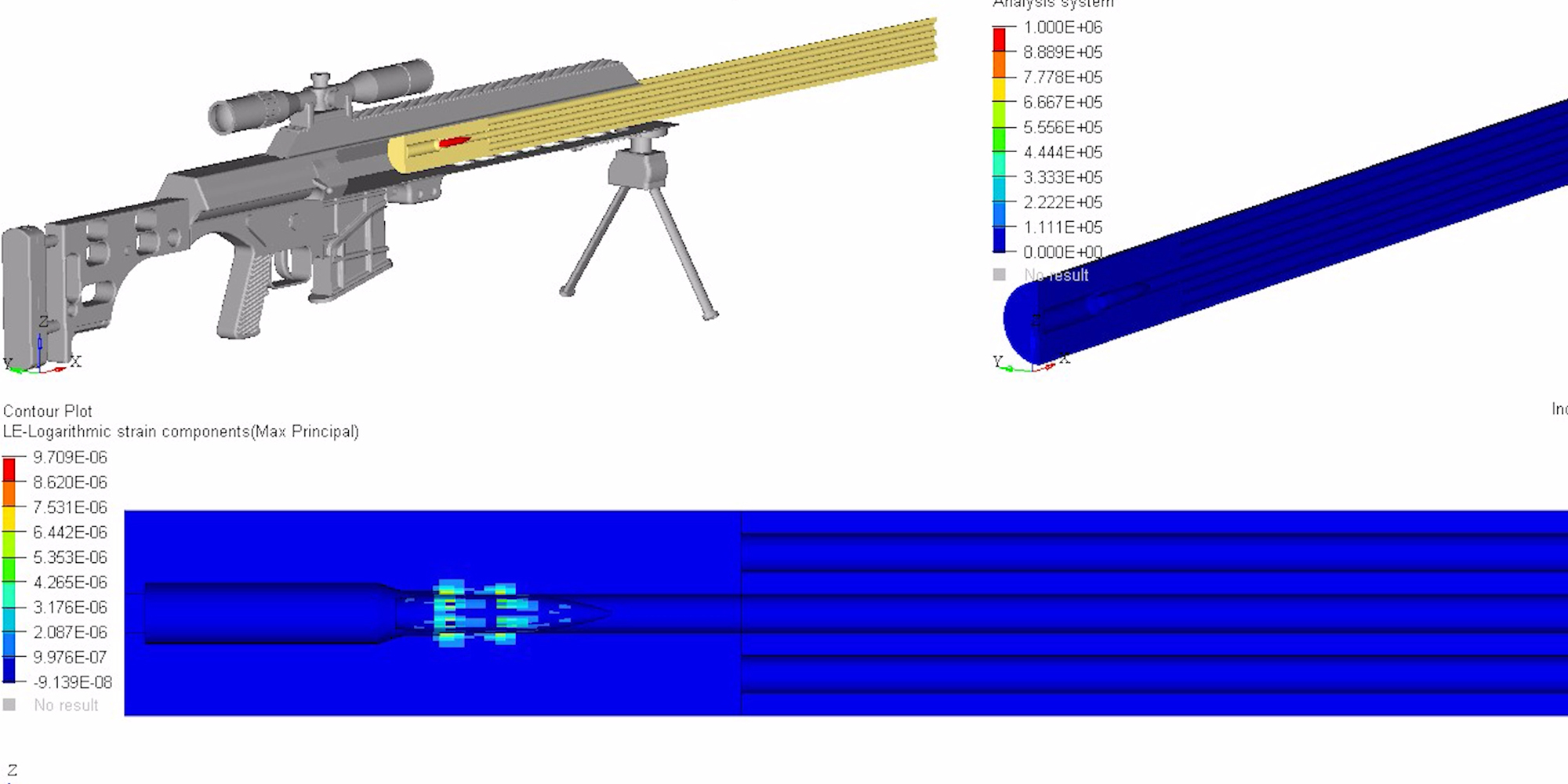
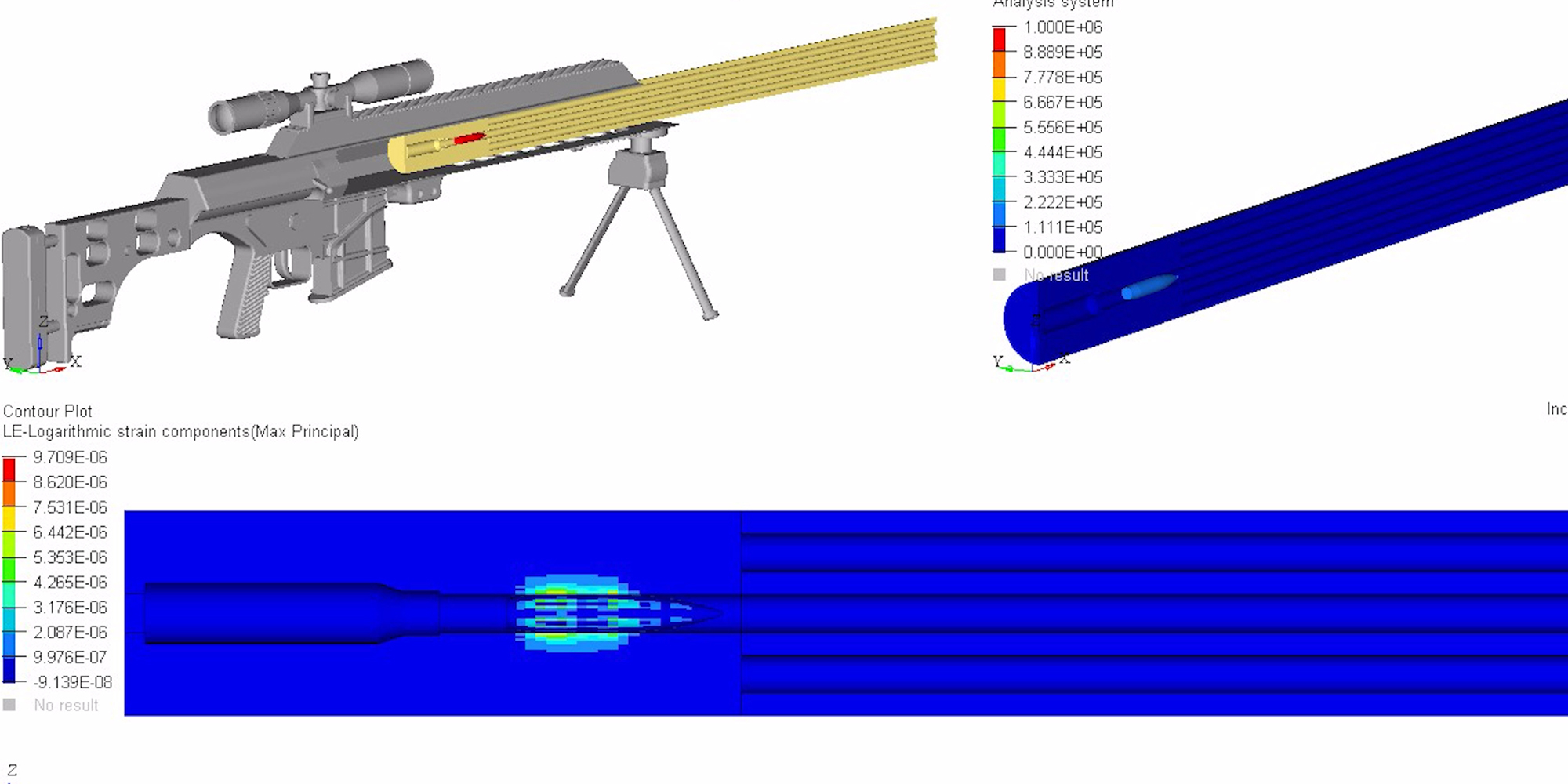
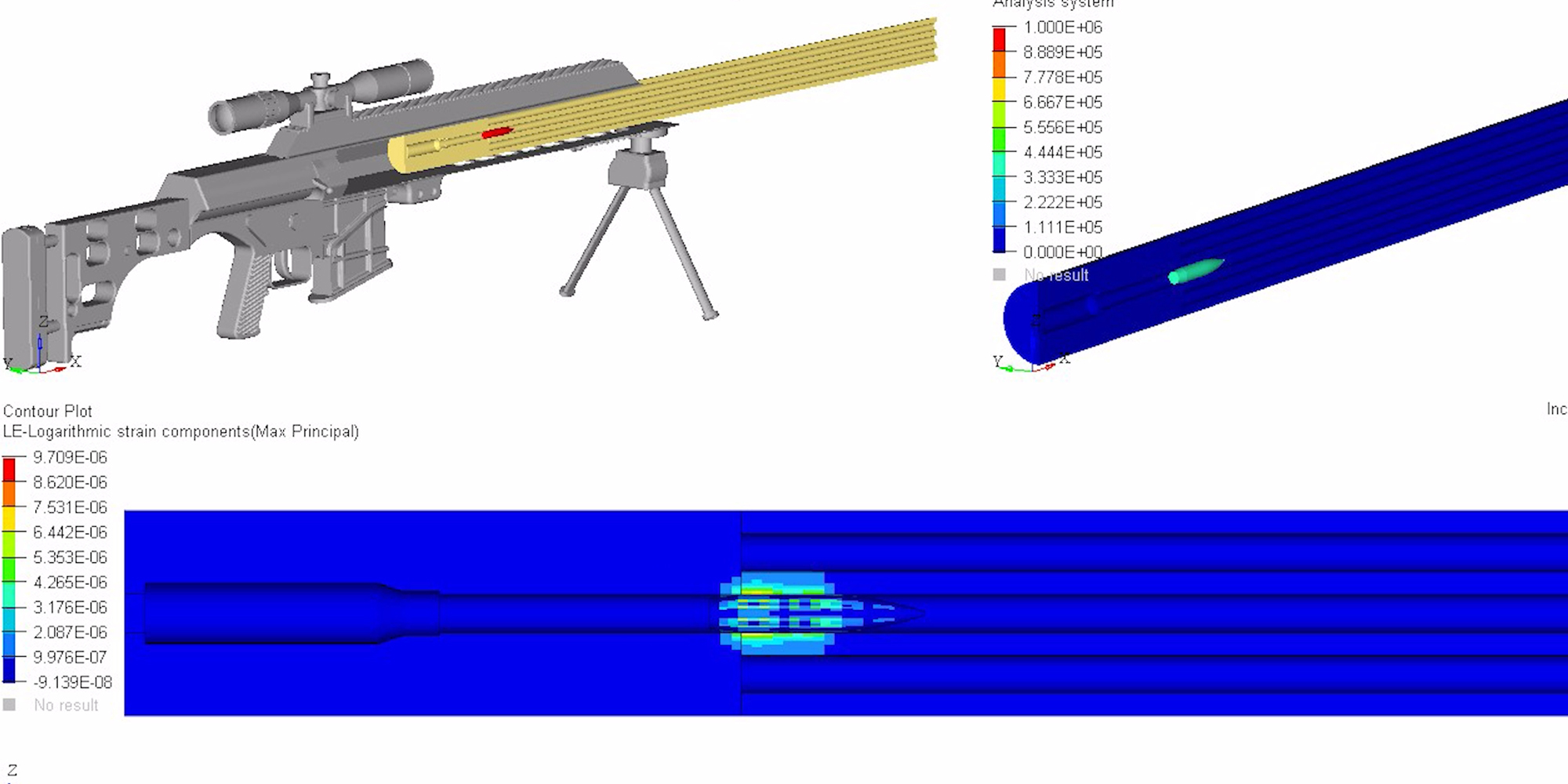
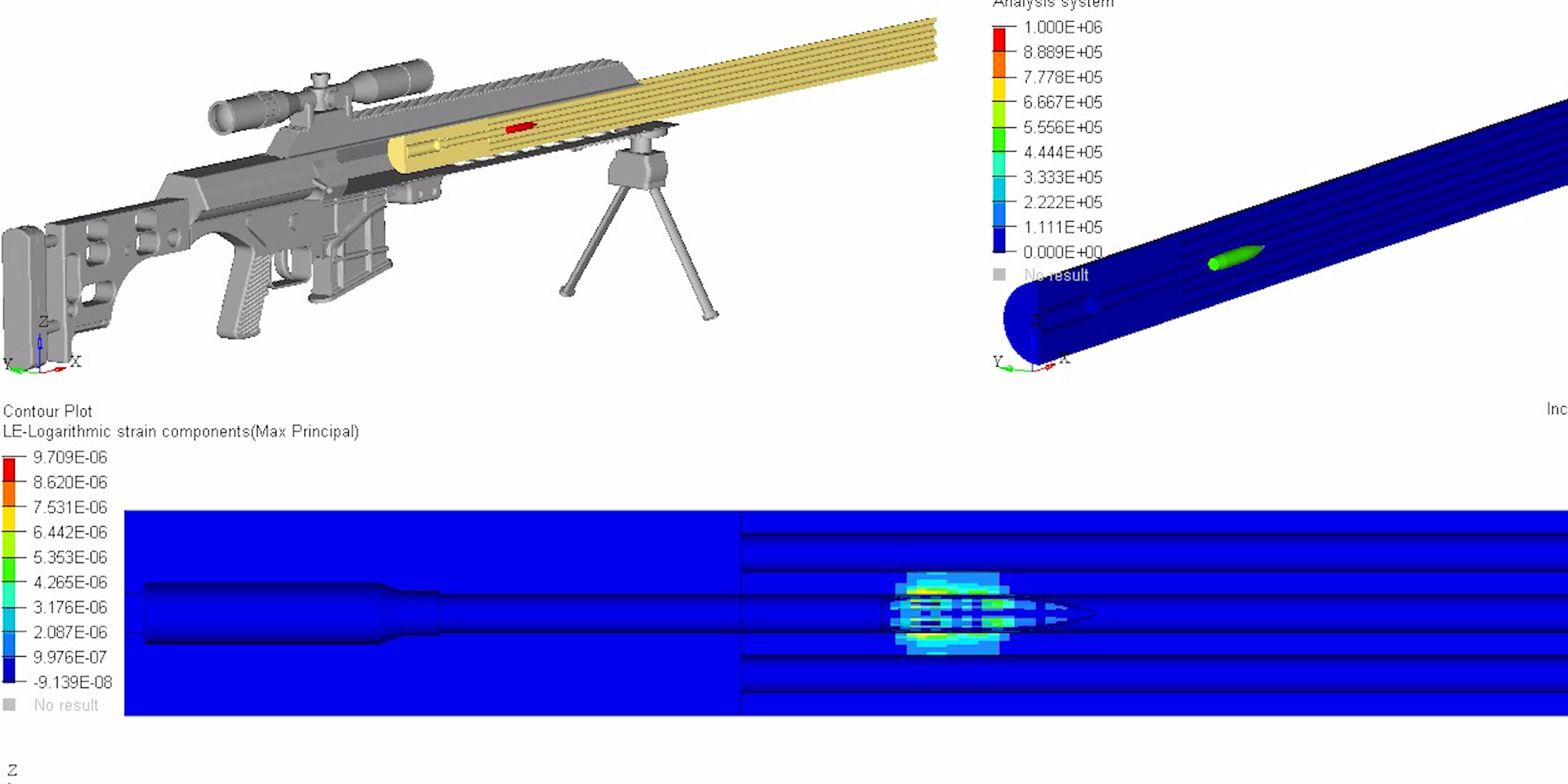
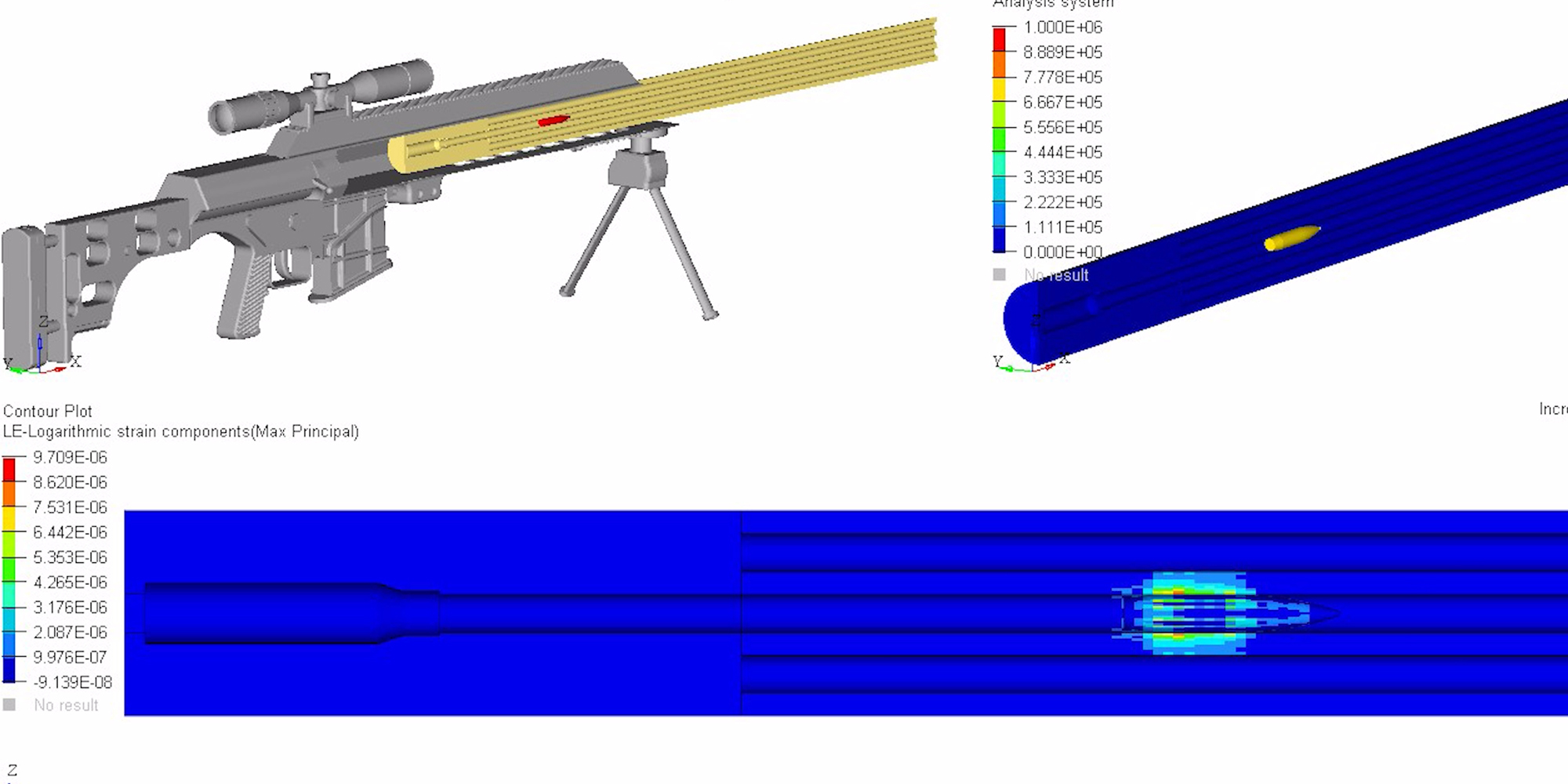
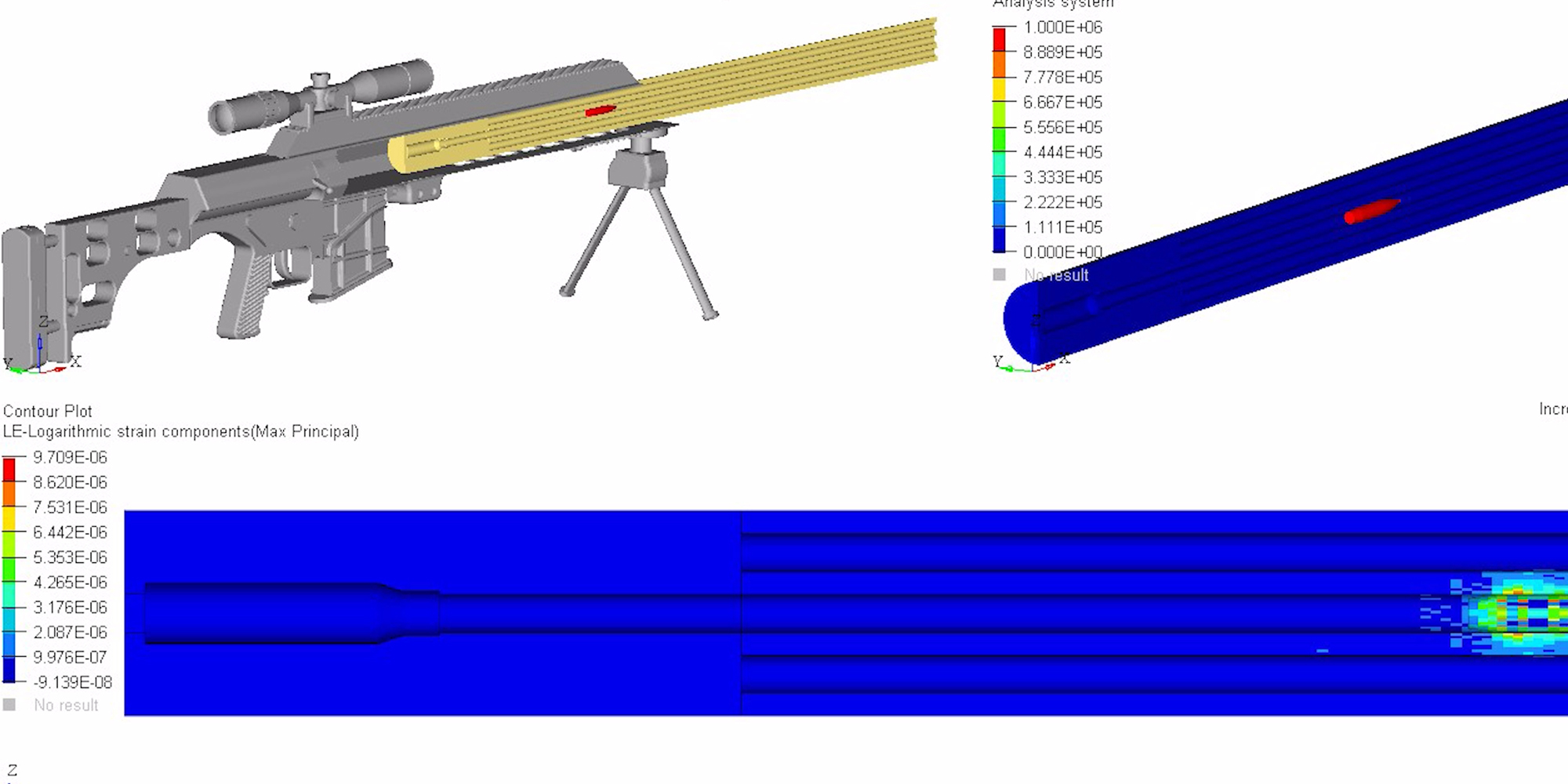
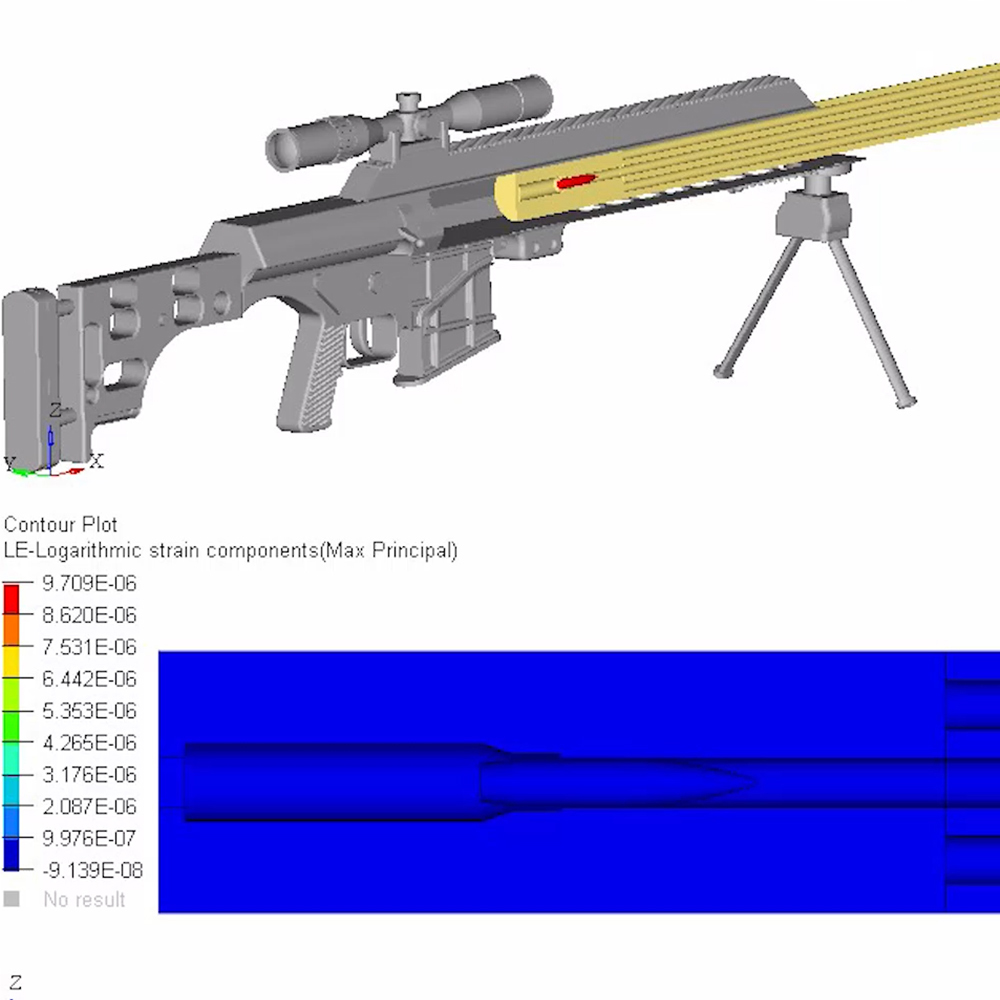
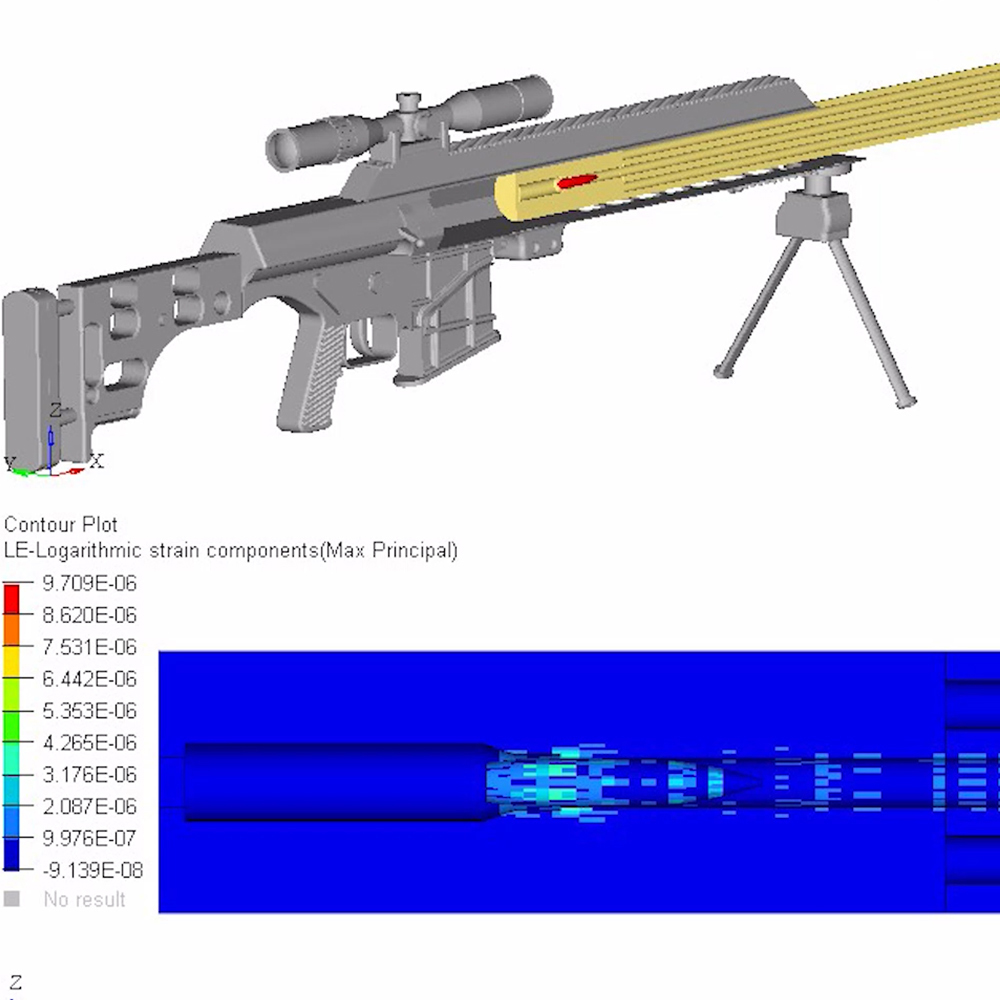
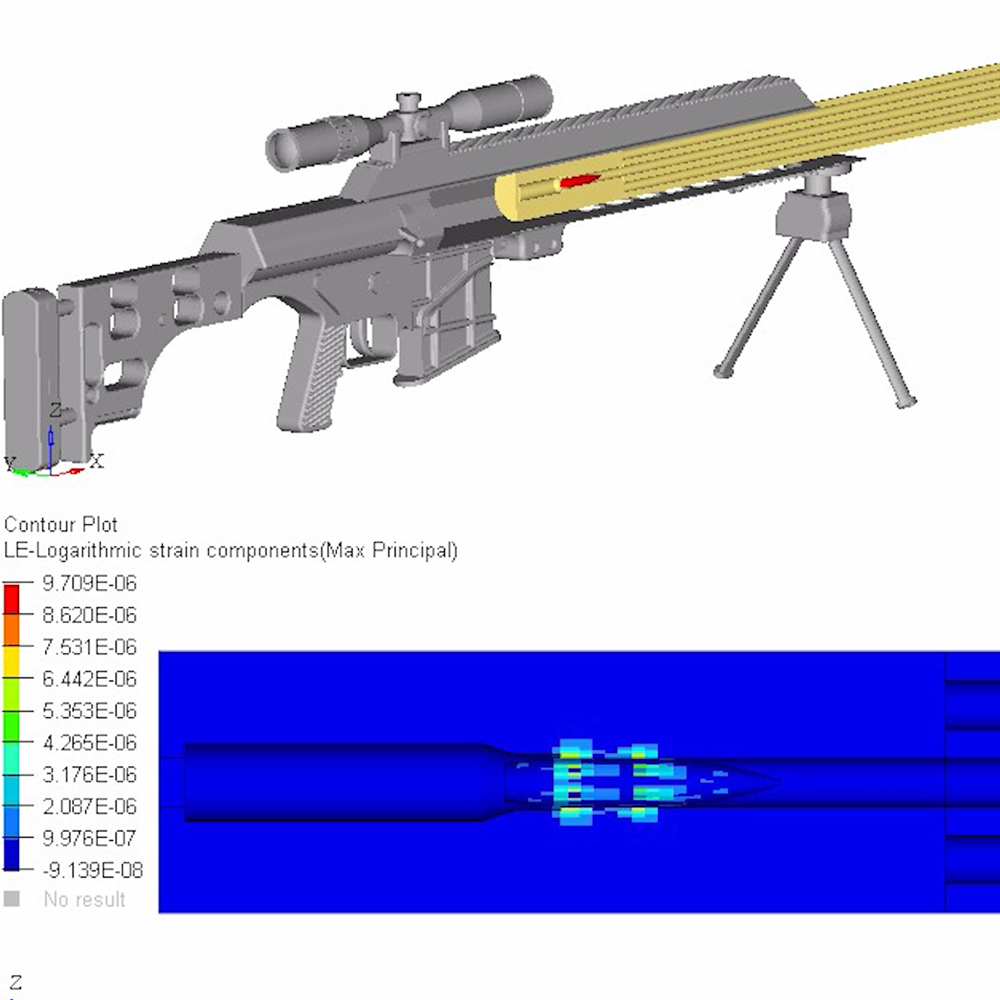
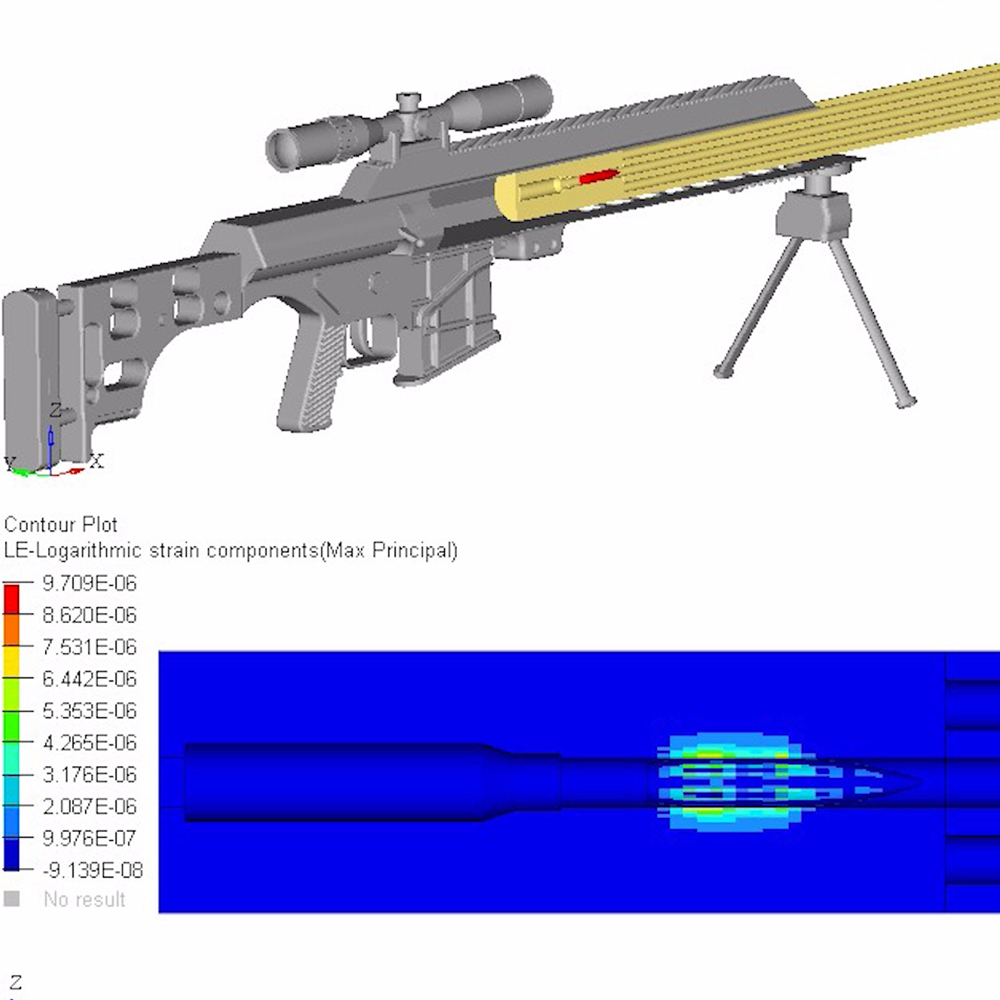
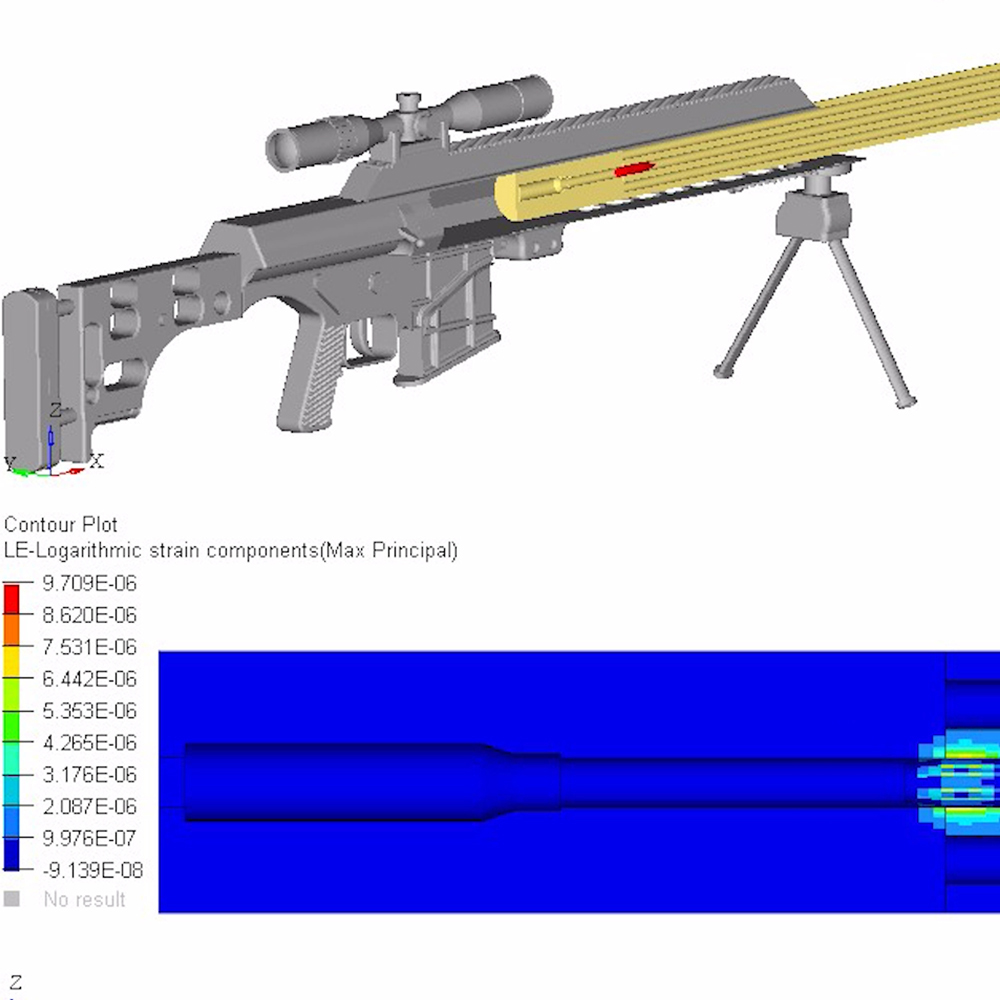
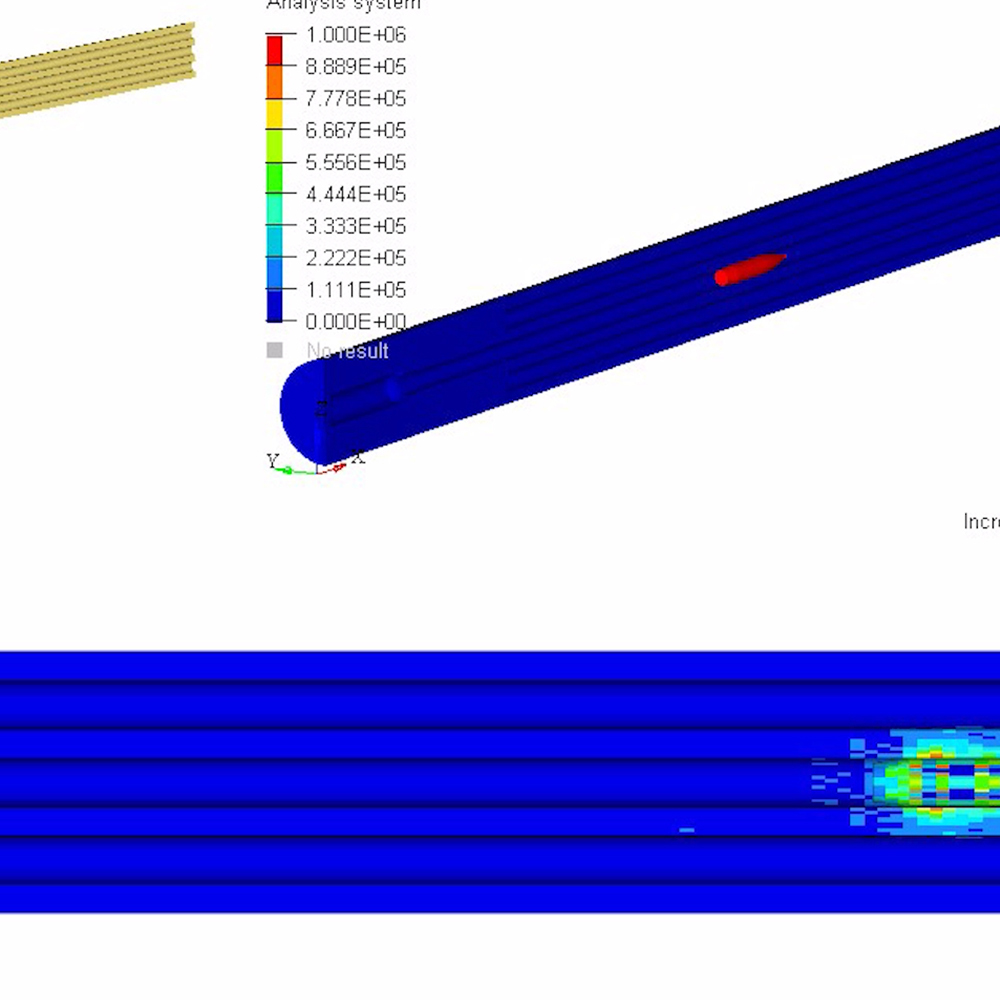
To better visualize a barrel’s physical response to waves, the following models and simulations are accredited to Al Harral, whom performed engineering and structural analyses on complex systems for 30 years at Lawrence Livermore National Laboratory, a government R&D facility. Analyses utilized LS-DYNA Finite Element Code, a powerful program for analyzing the dynamic and static loading of structures.
The following FEA simulations are used to evaluate the Vibration Mode and natural frequencies of a rifle barrel with a straight bore and where the displacements are greatly amplified so the shape change can be easily perceived. Click here for more research and data collection on barrel harmonics. The simulations show “forced deformations from the high pressure gas and recoil cause the muzzle to change where it is pointing at the target when the bullet exits the muzzle (….) The recoil and bullet motions ‘pulls’ the rifle barrel to a new shape.” – Al Harral’s 3-D Finite Element Analysis of a Barrel’s First Few Vibration Mode Shapes and Frequencies. Hence, a barrel with superior stiffness will exhibit less flexion just from pressure and recoil alone. Further, the depicted simulation shows “The vertical amplitude of vibration is more heavily excited than the horizontal vibration, because the center of gravity of the rifle is located below the barrel’s center line and the bullet’s travel down the barrel causes a vertical turning moment about the rifles center of gravity. [Making] the vertical vibration most important” – Al Harral’s Barrel Tuner Vibration Analysis. Again, these simulations assume a perfectly straight bore for simplification.
The simulated 6mm rifle assumes a 22″ 416 stainless barrel with no rifling and straight taper from 1.24″ at the breach to a 0.935″ DIA at the muzzle. The modeled barrel, action, stock, scope, scope mounts, brass weight, etc. came within approximately 7oz of the real thing. The FEA calculation for vertical POI often came within 0.1-MOA or less of real test results.

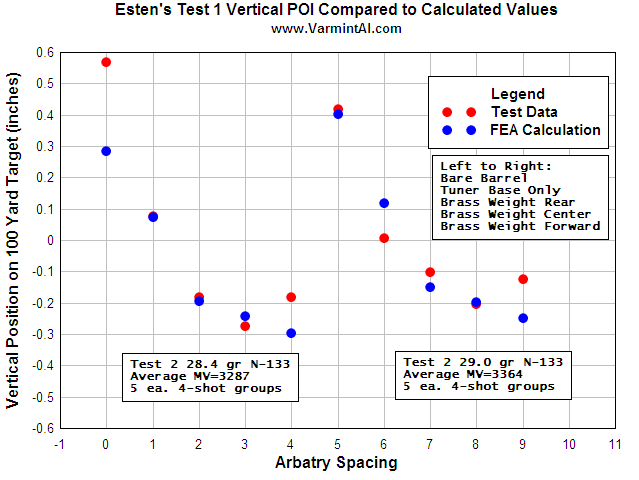
Mode 1
82Hz

Mode 2
406Hz

Mode 3
1050Hz

Mode 4
1756Hz

Mode 5
1984Hz

It is important to note, while modes 1, 2, and 3 are shown in a single plane, they can exist in other planes, and exemplary modes 1-5 are all excited simultaneously firing a round. While the higher frequency modes have extremely small amplitudes, it is mind boggling trying to visualize just these five modes acting at the same time, let alone more, each having a unique affect.
Mode | Frequency (Hz) | Mode Description
Mode #1 | 82 | Cantilever Bending
Mode #2 | 406 | 1 Node Bending
Mode #3 | 1050 | 2 Node Bending
Mode #4 | 1756 | Axial Extension
Mode #5 | 1984 | 3 Node Bending
The above simulations demonstrate how harmonics manifest as physical movement along the barrel’s length. The amount of resistance a shape can exert to bending about its geometry on a particular axis is its second moment of area, and this is dependent on the area and material distribution to the axial moment. Cross-sections of an object that locate the majority of the material far from the bending axis have larger moments of inertia, making said cross section considerably more difficult to bend when force is applied. This is one reason I-beams and not bars are commonly used in structural applications, and since Structural Barrels are analogous to I-beams reinforcing the bore in multiple planes, this creates a geometry that resists bending in multiple planes induced by harmonic resonance. Click here for a mathematical and geometric proof for a Structured Barrel’s superior stiffness compared to a standard barrel of the same mass.
Mathematical Stiffness Proof
Second Moment of Area (J) = ∫ r² dA; where r² = x² + y² and dA = 2π • r dr
J = ∫ r² • 2π • r dr = πR⁴/2
Perpendicular Axis Theorem Jz = Ix + Iy
Ix = Iy = πR⁴/4; barrels are a symmetric object
Second Moment of Area per Unit of Area | Rod (barrel) and Tube (Structured Barrel)
SRod = IRod / A; where A is the area πR² = R²/4
SCyl = (IRod / A) – (ICyl / A) = R²(1+x²)/4*
*As the x limit approaches 1:1 to radius R in SCyl, a tube will be 2x as stiff. However, this also requires an infinitely small radius difference. Nevertheless, these equations prove a body of equal mass positioned farther from the bending axis has a larger moment of inertia, making it more difficult to bend, which is further corroborated by an aeronautical CEL analysis that found a simulated barrel exhibited 56% more stiffness for the same weight.
UNDERSTANDING BARREL FLEXION AS HEAT
Flexion and Energy
Force is an exemplary load impulse. The equation to describe force is the multiple of mass and acceleration, the rate velocity changes in respect to time. Since barrels have mass, the work done to accelerate a barrel onto a sinusoidal wave about its center axis via tensive and compressive forces requires energy. This is described by the below equations:
v = x/t
a = dx/dt (rate of change)
F = m•a
W = F•Δx
ΔK = W
K = Energy (kinetic)
Energy and Temperature
Since energy is proportional to the work that acts on a system from an initial state to a final state (the First Law of Thermodynamics) and the Law for Conservation Energy dictates energy remains constant and is neither created nor destroyed, the work done on a barrel to accelerate it about its center axis due to flexion during firing or after the bullet exits the muzzle requires massive energy. Friction caused by (barrel) atom/particle acceleration creates heat, thereby raising barrel temperature. Even though each atom/particle is not vibrating at the same rate, described by Maxwellian distribution, it is also important to note the increase in thermal energy raises all of the individual (barrel) atom/particle vibrational speeds as an average, even though the medium as a whole will consist of multiple heat gradients along the barrel’s entire length.
Energy and Waves
Thus, as a barrel’s thermal energy increases, its density (D = M/V) also decreases due to thermal expansion, the tendency of matter to change in shape, volume, and area in response to changes in temperature. This expansion is uniform per calorie, but not uniform about the barrel due to many differing temperature gradients about the barrel’s length. Since the mass of the barrel remains unchanged but the overall distance between each atom/particle increases per Maxwellian distribution, thermal expansion constantly changes then tendency for the barrel to conduct waves as the distance and associated time for one atom to collide with another atom to relay a frequency changes gradient to gradient.
Variable Heat (Q)
While heat variable Q has minimal effect on the system’s rigidity at minimal round counts, extended firing sequences adds non-linear heat values Q₁ + Q₂ + Q₃ + Qₙ into the system causing the barrel’s resistance to flexion to become increasingly more susceptible to flexion due to changes in material stiffness, which is affected by temperature. An example of this is identifying groups opening, losing both precision and accuracy, on extended round counts. The prime temperature gain Q₁ describes detonation, pressure, and friction, but each subsequent Qₙ value segways into increasing contributions of thermal energy from the work done to whip the barrel at greater and greater amplitudes due to particle/atom friction.
Material Failure
Therefore, the work converted into thermal energy not only increases atomic vibration affecting material stiffness (modulus of elasticity) and other atomic, mechanical, vibrational, and thermal properties, but it changes barrel’s response to frequency and force load. Once a resulting force impulse wrought by flexion exceeds the material stiffness of an area provided by its temperature moment, material failure ensues.

CORRELATING BARREL FLEXION TO EXTERNAL BALLISTICS
Non-linear Acceleration
The work acting on a barrel to accelerate it about its center axis can also cost valuable kinetic energy (K = 1/2•m•v²), convertible into velocity, as projectiles must accelerate through a dynamic system. This causes irregular stuttering acceleration as work is done to momentarily straighten an imperfectly straight bore under non-uniform load. Otherwise, this assumes an absolutely rigid system with zero energy lost in the surrounding system, which is impossible. “The barrel [itself] is initially slightly deflected downward due to gravity [torque]. When the round is fired, the pressure also tends to straighten the barrel like a Bourdon tube in a pressure gauge. As the barrel straightens, it over shoots in the upward direction and this adds to the excitation of the Mode 1 vibration. As a side note, the axial extension vibration mode is also probably heavily excited.” – Al Harral’s Barrel Tuner Analysis.
Ballistic Coefficient (BC)
Accelerating the barrel about its axis not only costs energy, but it can also affect BC, the ability for a projectile to resist drag. The following is an exert from Sierra Bullets 2.4 Lessons Learned from Ballistic Coefficient Testing:
“Theoretically, the BC of a bullet depends only on its weight, caliber and shape. But in a practical sense, the measured BC of a bullet also depends on many other effects. The gun can affect the measured BC value in two important ways: spin stabilization and tip-off moments. A bullet is gyroscopically stabilized by its spin, which is imparted by the rifling in the barrel. If a bullet is perfectly stabilized by its spin, then its longitudinal axis (which is also its spin axis) is almost perfectly aligned with its velocity vector. If a bullet is not perfectly stabilized (which is usually the case), the bullet may not be tumbling, but its point undergoes a precessional rotation as it flies. In previous editions of Sierra’s Reloading Manuals we have described this precessional rotation and have called it “coning” motion to aid in mental visualization of the motion. As the bullet flies, the point rotates in a circular arc around the direction of the velocity vector. Coning motion results in increased drag on the bullet, and any firing test method then yields an effective BC value for the bullet that is lower than the theoretical value. We have never been successful in accurately predicting BC values, or determining these values by any method other than firing tests.”
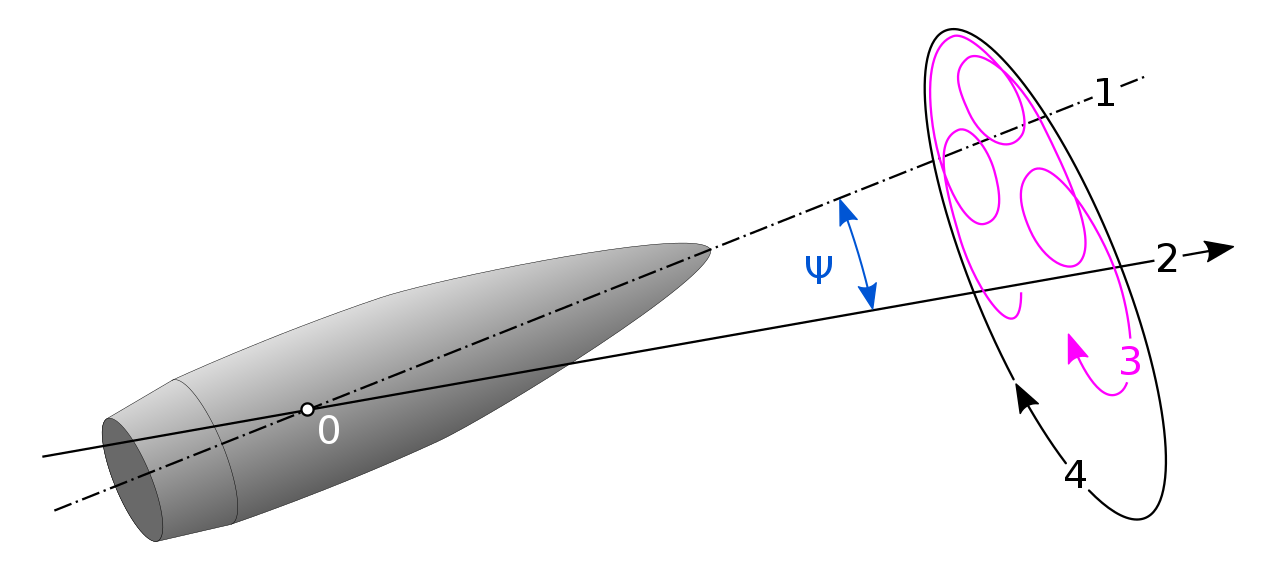
1. Longitudinal axis
2. Velocity vector
3. Nutation
4. Precession
ψ Yaw
Image credit
“Not only is the muzzle exit angle changing in time, but the muzzle is also moving in the vertical direction while the bullet is traveling down the barrel. When the bullet exits the muzzle, the bullet will have the same velocity as the muzzle.” – Al Harral’s Barrel Tuner Analysis. One of the most basic evaluations, in finite terms, is given bullets have length, they cannot be evaluated as a finite point. Thus, bullets will almost always have nutation, precession, or yaw of some degree due to a barrel’s acceleration about its center axis. This is the precise reason load development consists of finding an amplitude where barrel velocity and the resulting tip-off moment is minimal.
DEFINING A STRUCTURED BARREL AND ITS ADVANTAGES
Solving the Problem
From the physics principles outlined above, we learn barrel stiffness is a driving component that determines how barrels are pulled off axis from gas pressure, recoil, bullets, bore contours, harmonics, and temperature is an increasingly contributing variable affecting the overall system, especially at extended round counts. Increasing structural stiffness eloquently solves these critical elements as an improvement in a barrel’s second moment of area also reduces the potential for work and thermal energy to act on said barrel. TACOM HQ accomplishes this feat via a Structured Barrel, a large diameter barrel with aftermarket interior and exterior finishes that significantly increases stiffness weight for weight. Structured Barrels distributes its material mass farther from center to exude larger moments of inertia, making them significantly more rigid, despite having a weight comparable to that of a standard barrel, sometimes lighter.
2023
• .22 NLR | 1st Place Chris Baxter
• ELR Heavy – Global Ranking | 1st Place Chris Schmidt
• Review import/export code(s) and requirements here.
Advantages
• Structured Barrels are significantly stiffer than a standard barrel. See INTEL > How it works for details.
• An independent analysis using MSC/NASTRAN, a state of the art program in the aerospace engineering world, found it was 56% stiffer than a standard barrel of the same weight.
Videos:
Harmonic Proof
Mathematical and Geometric Proof
• Structured Barrels are 21% lighter than a standard barrel of the same stiffness.
• Larger the outer diameter (OD), greater the Structural benefits. Smaller the OD, lighter the barrel at the loss of additional rigidity.
• Weight is comparable to a standard barrel if matched.
• Structured Barrels are 38% lighter than a standard barrel with the same frequency.
• Requires minimal load development.
• Structured Barrels exude +3-500% more surface area compared to a standard barrel, yielding less mirage, barrel drift maintaining material stiffness, and velocity migration at extended round counts.
• Improving both structural stiffness and temperature resistance conserves superior material stiffness through pressure, heat, and force cycling. Once a resulting force impulse wrought by flexion exceeds the material’s stiffness provided by its temperature moment, material failure ensues, and extended firing sequences strain material properties. See INTEL > How it Works for details.
• First shots after break-in | Mark and Sam After Work
• Experience and analysis | Rex Review
• Structured Barrels worth it? | Chase Stround DPI Precision and Chris Schmidt
• Ladder test | Coastal Precision
• Throat erosion comparison | Coastal Precision
• CEL aeronautic program analysis | TACOM HQ
• Independent user compliation | TACOM HQ
Finishes
• A deep-hole drill pattern around the bore that takes advantage of axial compression.
• Axial compression describes the tensive and compressive forces exerted on an object to make it bend. Tubes are simple structures that oppose this event due to its ideal structural stiffness. AUX drilling creates a host of tubes that work in series to reinforce the bore. As one hole bends, one side undergoes tension and the other compression. This triggers the hole opposite of it in the pattern to undergo compression and tension, 180 degrees out of sync, and opposing force vectors cancel applicable x-y magnitudes. This significantly reduces supersonic flexion and the work done to generate thermal energy.
• AUX drilling is not a sleeve. Thermodynamic expansion coefficient deltas from different materials induce systematic stress and changes in vibrational frequency.
• Vent holes are configured in a spiral pattern near the throat induce concentrated convection cooling.
• Negative pressure generated at the muzzle pulls columns of high-velocity air through the entire neck of the barrel with each shot, cooling it from the inside-out. Velocity may exceed 50 fps (10 m/s).
*Suppressors alter the precise location of this low-pressure zone and will dampen this phenomenon.
• Aligns metallurgic molecular structures to reduce material micro voids, tears, and or overlaps for more uniform material stiffness and harmonic stability.
• Offset radii cored perpendicular to AUX drilling pattern around the chamber to dampen vibrational frequency.
• Extracts significant weight while maintaining rigidity.
• Multi-directional threads cut in randomized sequences of length and pitch to resist surface translated harmonics while increasing heat dissipation.
• Adds more surface area for greater temperature resistance.
• Sandblast – Creates millions of microscopic surface depressions to increase surface area and reduce glare (ideal for snipers).
Specifications
• Click here to select a final, max barrel diameter by caliber.
• Larger the diameter, greater the Structural benefits. Smaller the diameter, lighter the barrel. Prioritize performance or weight. Final diameters are dictated by caliber and length. Change the length for more finish options.
• Select a final, Structure diameter per stock or chassis barrel channel.
- Assuming a high-end lapped barrel, use Tubb’s break-in bullets from the TMS kit – caliber specific. Five sets of bullets will be provided with your kit.
- Load ten bullets at 75-85% of charge and lube each bullet with Imperial Sizing Wax, Hornady One Shot, or equivalent to reduce seating pressure. Set seating depth so the bullets do not engage the rifling.
- Thoroughly clean the bore using a brush and patches to remove particulates; this may require significant brush-force due to adhesion forces.
- Shoot five rounds.
- Thoroughly clean the barrel using a brush, patches, solvents, and detergents for 30-60 mins until you get a clean patch. This prevents driving unwanted material into the barrel’s porosity.
- Shoot remaining five rounds and repeat step 5.
- Shoot five Burnishing Bullets and repeat step 5.
- Shoot 10 rounds using your specific bullet at 85% charge (metallurgies vary between manufacturers) and repeat step 5.
Complete. At this stage, there should be a lead into the lands and any burrs from throat operations removed.
*DISCLAIMER: Failure to follow these steps may cause inaccuracies, and voids any guarantees associated to Structured Barrels®.
• Repeat steps 1-5 as necessary for tune intervals will vary according to caliber, pressure, and bore conditions.
• Borescopes are highly recommended to guarantee a comprehensive and consistent bore cleaning.
Standard vs. Structure
• Structured Barrel Versus Standard Using a Swithlug
Jul 18, 2018
• TACOM HQ’s Structured Barrels Beat the Heat
Sep 6, 2018
• Studying Barrel Drift (Structured vs Conventional Barrels)
Jul 21, 2022
10x 5-Round Strings per Barrel Manufacturer – Total 50 Rounds
Temperature Readings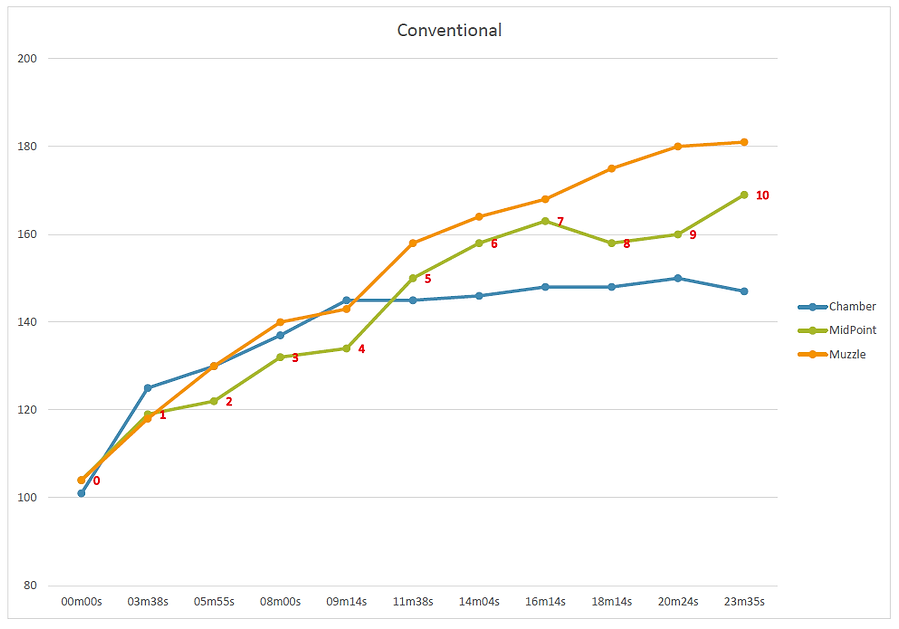
Temperature Readings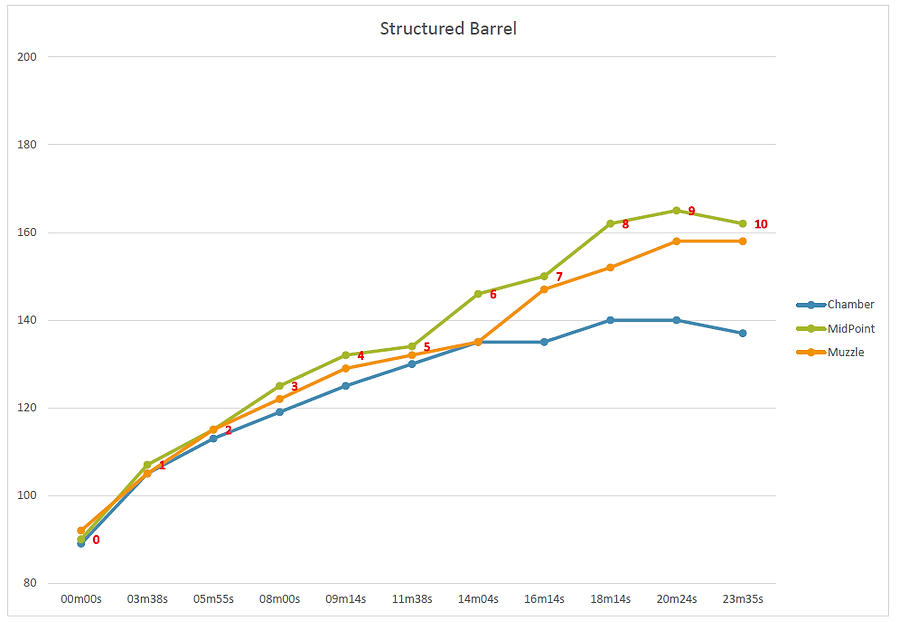
• Vudoo .22
“The first 10-rounds with the SK were one hole. One thing became very obvious to me is the ES/SD impact shows immediately, but that was it. The rifle wants put everything in the same hole. It’s like watching a video game through the scope. No recoil, no movement, nothing just deadness.
Groups at 100-yds | POA 2/10ths high:
+ 1st row CX .001RO | Avg .1675″
+2nd row Midas+ no RO | Avg .268″
+3rd row XACT no RO | Avg .276″
+4th row Tenex no RO | Avg .272″
*RO – Run out
Corollary data:
CX 0.001RO | Avg 1065 SD 6.7
M+ | Avg 1068 SD 11.4
XACT | Avg 1049 SD 8.9
Tenex | Avg 1107 SD 8.1
Δ58 FPS
Honestly, the rifle outperformed every ammo I fed it. It needs to go to Lapua and Eley for testing in their tunnels to find an ammo lot that will deliver the best SD’s. It was amazing shooting across the radar that I could tell based on where the impact went whether the velocity was high or low. I did have some ammo I was testing an Olympic runout gauge on, and the ammo performed best. And it was .001RO. I still need to shoot the .000’s I have, those will tighten up the group even more. Or at least the data of 20 years of research shows that for every .001″ of run out equates to 1/10th group size. The barrel is outstanding, and shows quickly the weak point is in the ammunition. Even though it’s Olympic ammo.
The velocity gained has been consistently 30fps, and that’s with a 4″ longer barrel than prior. ES has been cut in half and are consistently low single digits with match ammo. Shooting at a Dalt of about 7500ft in 95-deg weather, the Lapua SLR ammo was ~1150fps (spicy), but the groups at 200+ were incredibly tight.” – Chris Baxter
5-Round Groups from Four Different Manufacturers

Customer Rifle

“I finished the local season (.22 NLR) with a 777.5 point lead over my next closest competitor, who shot the same matches. The spread was roughly a fully match worth. The barrel was instrumental in being able to achieve the Expert Classification. I am the 16th person in the country to achieve it.” Chris Baxter closed the season at 8228.0 points, averaging 713.0 points per match. The next top four competitors averaged 6,994.8 points or 649.2 per match.
• Rounds 21-30x on 300 Norma with +1,800 documented rounds
1x Round every 30-35s at 100yds
Factory 208gr at 3,164 FPS
Ambient 58°F
Barrel temperature 110°F
Day 1
Day 2 (repeat)
• “Loving this barrel but DAMN has it sped up my MV’s. It isn’t a huge fan of my SK long range ammo that used to shoot 1075 consistently in 80 degree weather, it now shoots 1109. I tried some Eley Tenex that is rated at 1069 from the lot number but shoots 1130 MV’s in the same temp. Huge differences and I’d expect the barrel to speed up as it ‘breaks in’.
Lapua center X went from 1085 to 1133.9 avg, SK LR went from 1079 to 1109 avg, Eley TENEX went from 1080’s to 1130, Eley Tenex Ultimate went from 1080’s to 1112.5 avg. Interestingly, SK Match maintained a 1057 avg which is barely over the low 1050’s avg it had before. All 30-shot strings for average in 81-degrees” – @76.binder

• World Record Extreme Long Range Shot 4.4 Miles
Sep 14, 2022
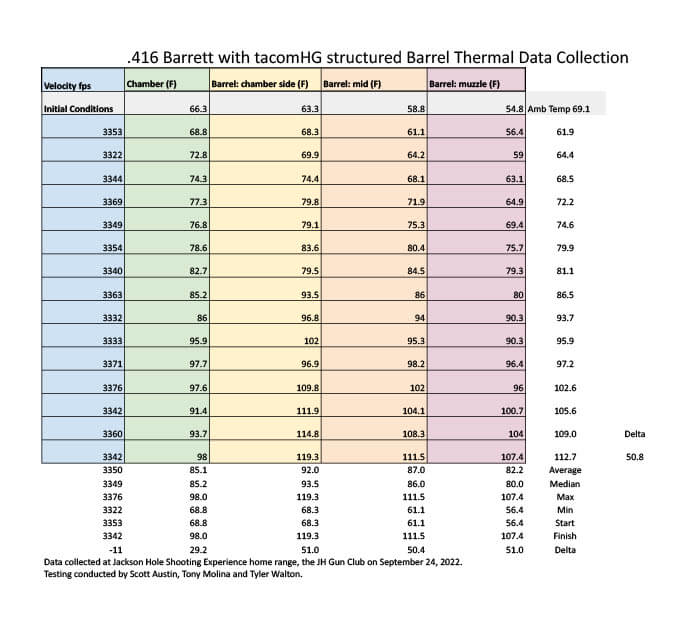
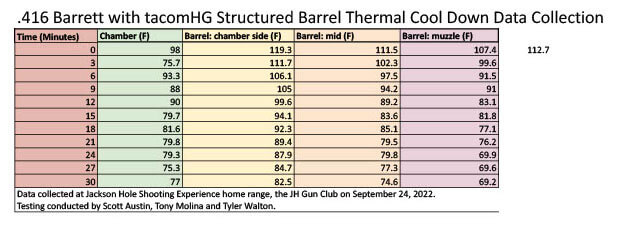
• TACOM HQ Structured Barrel Temperature Testing
Sep 24, 2022
15x Round Shot String .416 Barrett with ~40s Intervals
15x Round Shot String .416 Barrett with ~40s Intervals Cool Down
• 3,000 Round 6mmCM Structured Barrel


• 30-round Group from 3x factory ammos shot every 30-35s
Bottom group Sig Sauer 107gr Marksman
Middle group Hornady 108gr ELDM
Top group Barnes 112gr match burner



