TACOM HQ®
Command Results
CAGE 834B9 SAM GHMFLBP9GGM3
“Incoming fire has the right of way." - Unknown
Structured Barrel®
About
TACOM HQ is the leader in innovative, firearm accessories, and renowned for its cutting-edge products designated to enhance the modern warfighter. We are the proud creators of the Structured Barrel, a revolutionary, patented design so end users can shoot longer, run cooler, and mitigate recoil for quick, follow-up shots. Comprising internal and external geometries machined from a monolithic barrel blank, no other industry solution matches our rate for cooling and stiffness to maintain barrel stability in prolonged engagements. Structuring adds a massive +300% surface area and +50% more rigidity compared to a barrel of the same weight, so Structured Barrels demonstrate superior endurance in combat or competition. We add stability for reliability.
Buy Internally Structured Barrels (ISB)
At TACOM HQ, we idealize physics, rooting our research and application in engineering discipline. Click here for a complete physics detail. It is for this reason a Structured Barrel is one of the most highly sought after high performance barrels for sale in the industry, because its I-beam geometry generates +300% more surface for cooling, rapidly evacuating heat out of the system instead of relying on materials with different thermal expansion coefficients or mass to compensate. Unlike any other barrel available, this makes the chamber of a Structured Barrel uniquely the coolest section. The added heat dissipation also and distinctively preserves material stiffness as this property is temperature dependent. Since metal becomes more malleable with heat, Structured Barrels with its high surface-area-to-volume ratio exude greater endurance and overall life.
The I-beam geometry also serves to overcome flexion. Boasting +50% more rigidity than a barrel of the same weight, Structured Barrel’s large diameter, I-Beam, and other structural elements impart far greater resistance to forces generated by gas pressure, recoil, and bullet-barrel interaction. These forces work to simultaneously push, pull, stretch, compress, and twist the barrel in multiple planes, relaying the speed and magnitude of each displacement as a frequency and perceived as barrel whip, and this also generates a lot of heat through atomic material friction. The added rigidity ensures a more stable platform throughout recoil, mitigating thermal rise, and increases the accuracy of rapid, follow-up shots.
The combination of +300% more surface area and 50% rigidity work in concert to ensure Structured Barrels remain stable, every feature is purposely designed to optimize structural and thermal performance. This is all accomplished at a weight comparable to a conventional barrel. Click here for a barrel weight calculator. Whether in the field or at the range, Structured Barrels enable end users to engage targets through prolonged shot strings without compromise or concern, especially with mirage obscuring the target. This makes them a preferred choice for any serious shooter.
When choosing TACOM HQ, you’re not just purchasing innovative, cutting-edge gear; you’re gaining access to an entire team committed to your success. Whether you’re a military combatant, law enforcement officer, professional shooter, or an 2A enthusiast, TACOM HQ offers the next level in barrel technology for sustained performance. Contact us today to learn more about our product and how we can assist to unlock next-level efficiency.
Information Debrief
Advantages
Thermal Endurance
• Structured Barrels exude +300% more surface area for heat dissipation compared to a conventional barrel, so end users can shoot longer and run cooler. The high surface-area-to-volume ratio preserves material stiffness for greater performance in prolonged engagements and overall longevity, while also dramatically reducing mirage, barrel drift, and velocity migration. Click here to understand barrel flexion as heat, the effects of thermal expansion, and the deterioration of material stiffness at high temperatures.
Increased Rigidity
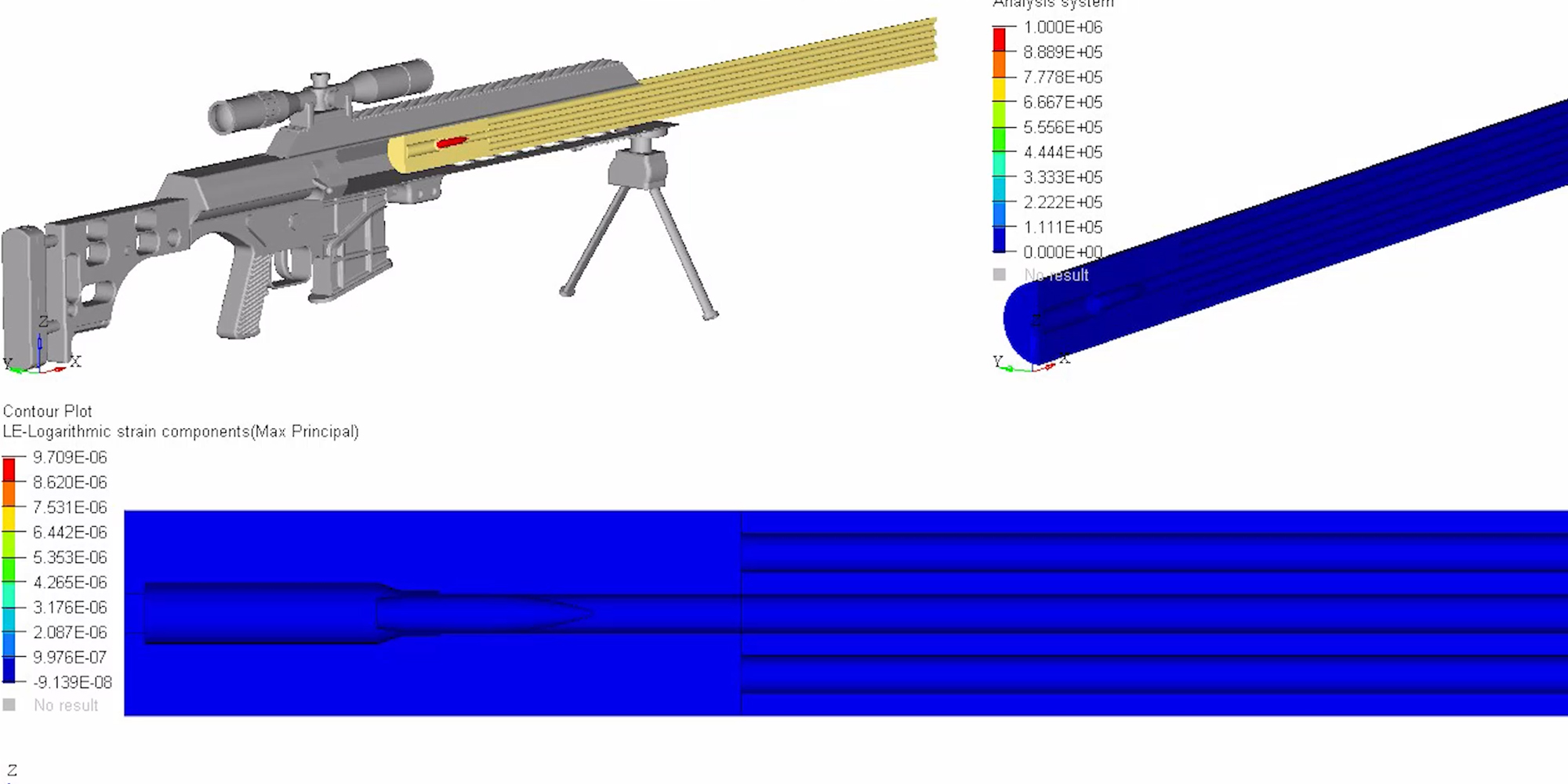
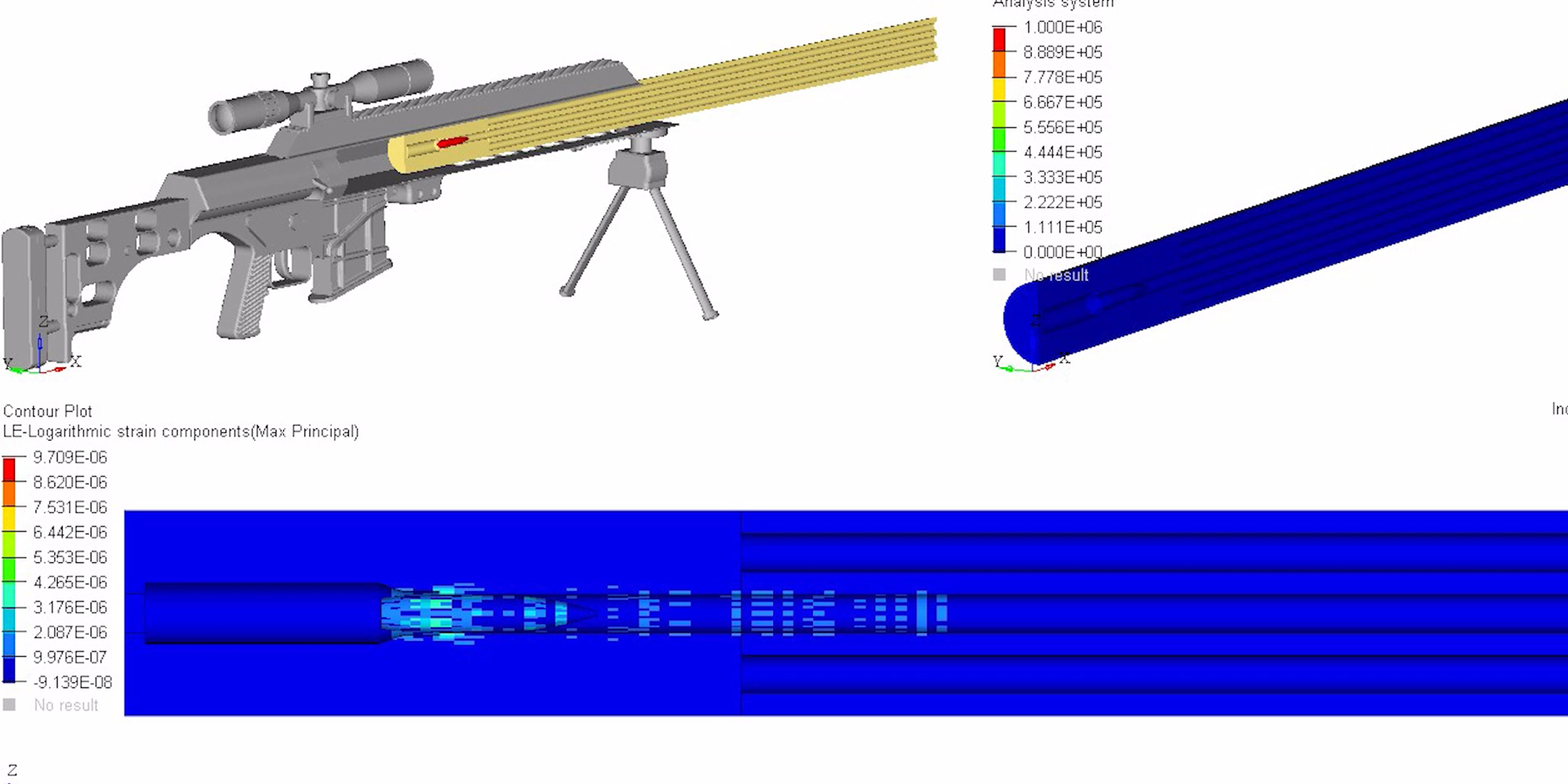
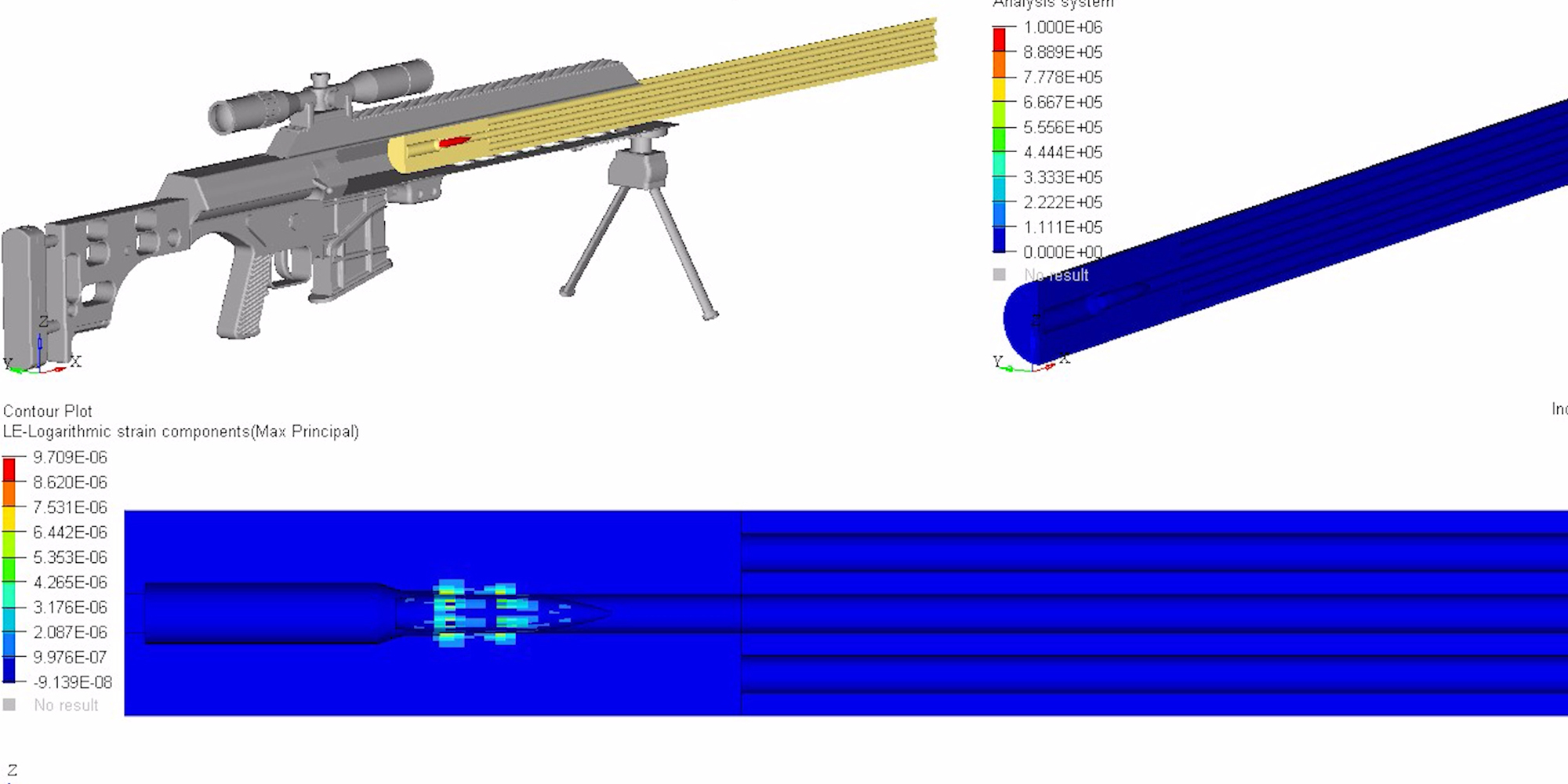
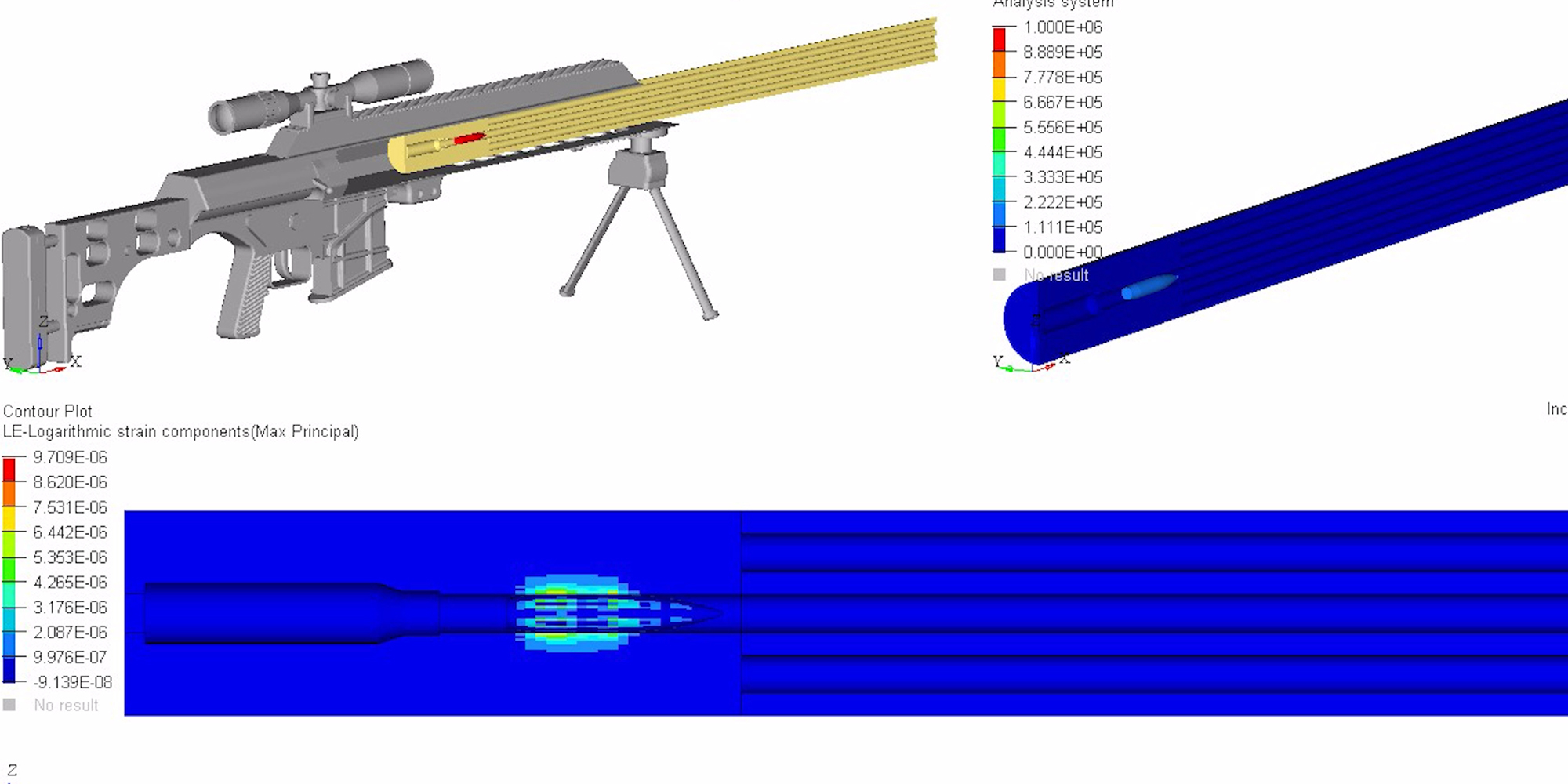
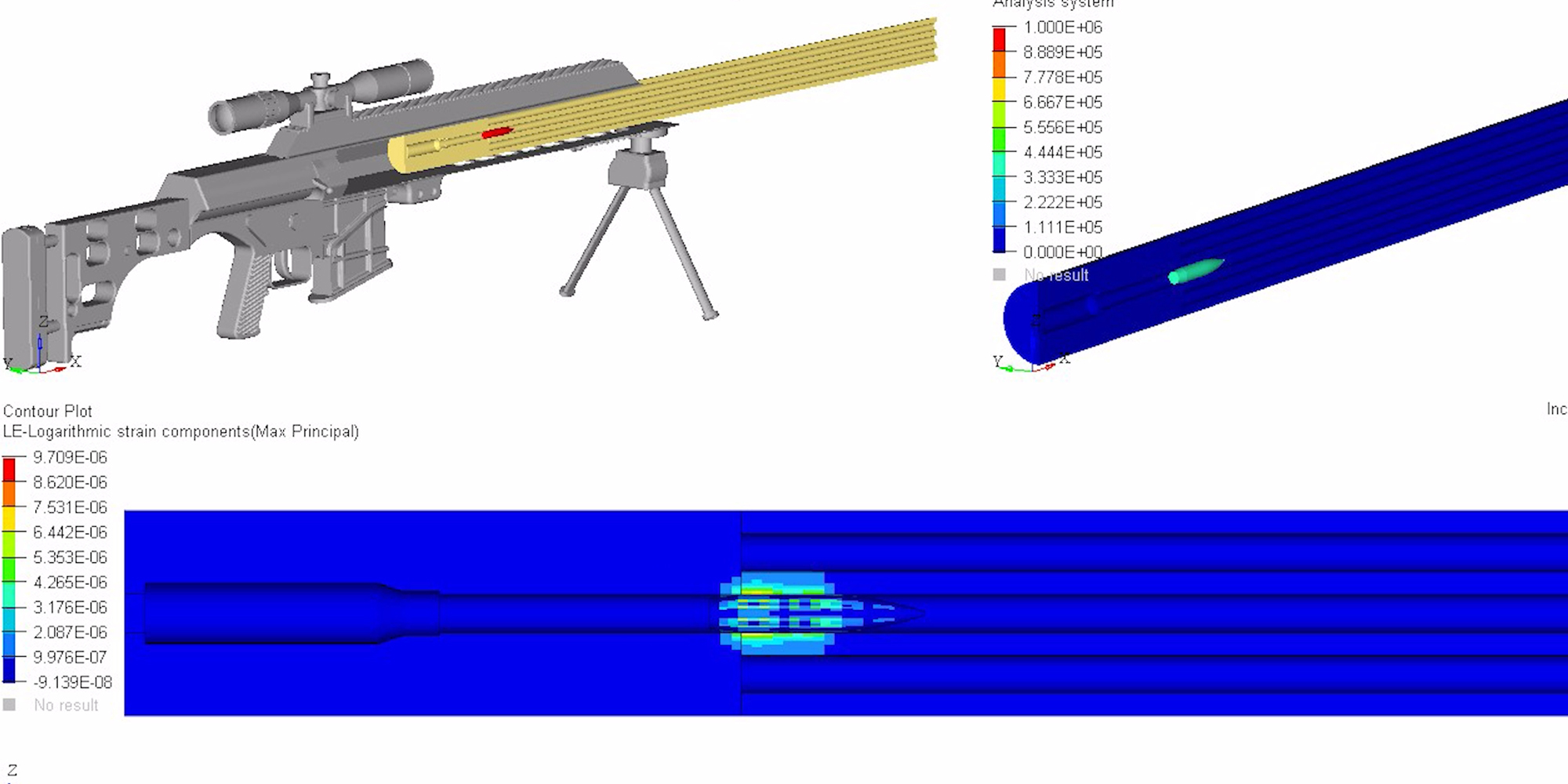
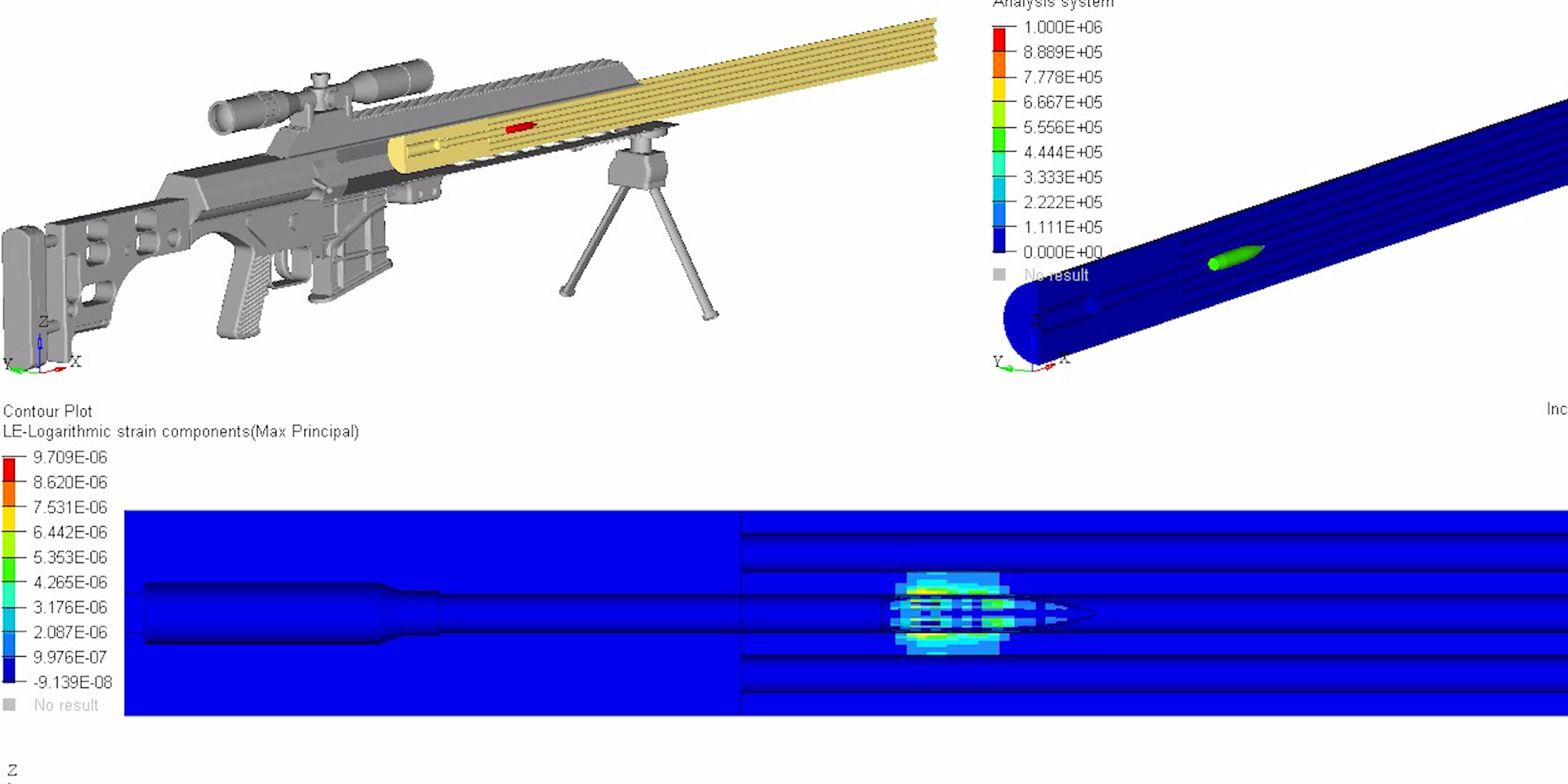
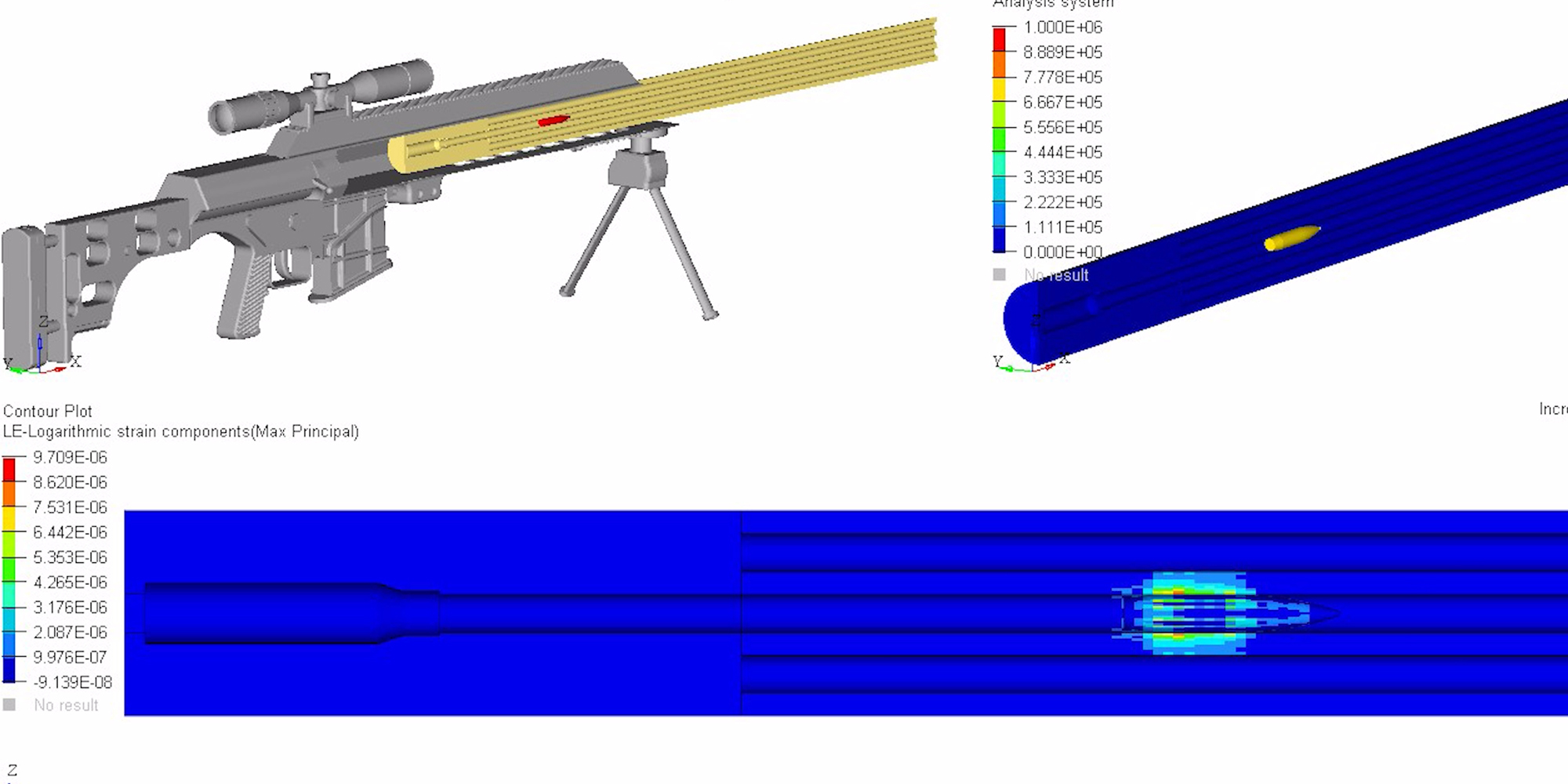
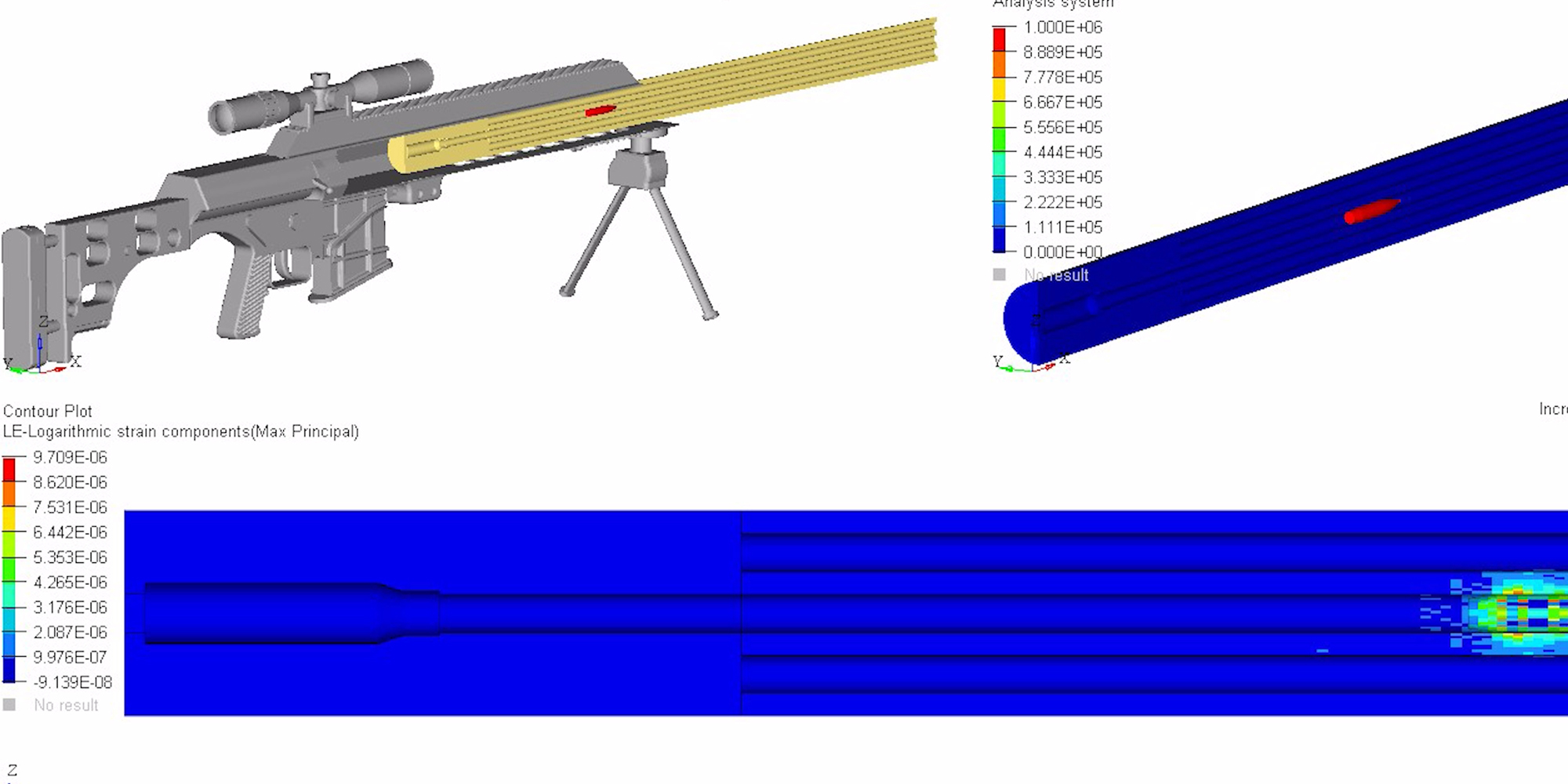
• Structured Barrels are +50% stiffer than a conventional barrel of the same weight, so end users can send faster, more accurate follow-up shots. The massive gain in rigidity was calculated in an independent analysis using MSC/NASTRAN, a state of the art program in the aerospace engineering world, and corroborated by various physics and engineering equations used to define an object’s second moment of area, or resistance to bend. Click here to understand barrel flexion as waves, the effects of waves on a body, and deflection resistance via second moment of area,
Minimal Weight
• Structured Barrels are comparable in weight to a conventional barrel, and 21% lighter for the same stiffness. Click here for a barrel weight calculator that simultaneously compares the weights of a bull, tapered, and Structured Barrel.
Ballistic Stability
• Precisely follows trajectories calculated by Kestrel with Applied Ballistics software with little to no truing and exhibits superior velocity SDs.
Finishes
I-Beam
• Deep-holes radially drilled around the bore of a large DIA, monolithic blank to harness axial compression.
• Axial compression describes tensive and compressive forces exerted on an object to make it bend. I-Beam drilling creates a host of tubes that work in series as an ideal structure to reinforce the bore. As one hole bends, one side undergoes tension and the other compression. This triggers the hole opposite of it in the pattern to undergo compression and tension, 180 degrees out of sync. The opposing force vectors significantly reduce flexion and the work converted into thermal energy.
• The I-beam pattern locates the majority of material far from the bending axis to withstand flexion. This creates a much larger second moment of area, which makes said cross section considerably more difficult to bend when force is applied.
Vents
• Vent holes configured in a spiral pattern near the throat induce concentrated, convection cooling. Negative pressure generated at the muzzle pulls columns of high-velocity air through the neck of the barrel with each shot, cooling it from the inside-out. Velocity may exceed 50 fps (10 m/s).
*Suppressors alter the location of this low-pressure zone, dampening this phenomenon.
Cryo
• Aligns metallurgic molecular structures to reduce material micro voids, tears, and or overlaps for enhanced material stability.
Dimple | Add-on
• Cores milled around the chamber and perpendicular to the I-Beam structure for vibration dampening and weight reduction.
Fallen Angel | Add-on
• Multi-directional threads cut at random lengths to resist surface translated frequencies and further increase surface area to +500% compared to that of a conventional barrel.
Sandblast | Add-on
• Creates millions of microscopic surface depressions for a matte finish to reduce glare (ideal for snipers) and increases surface area.
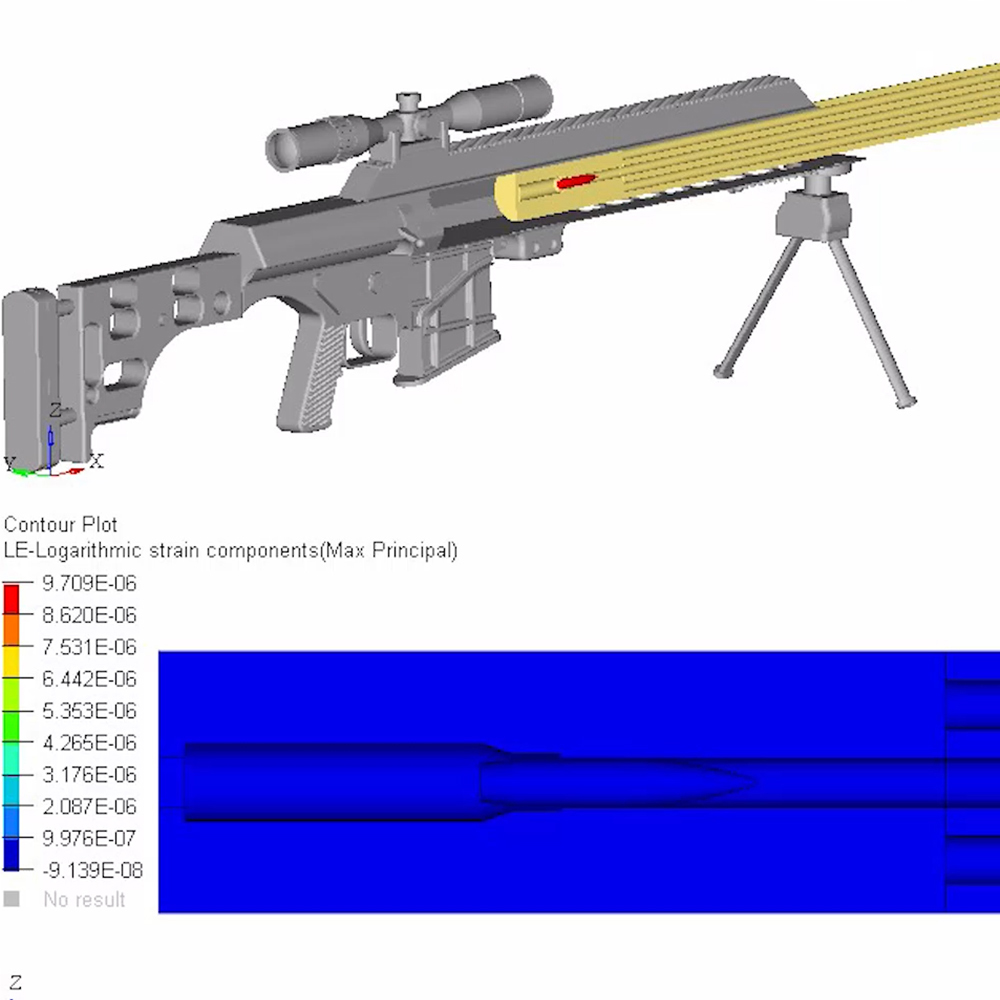
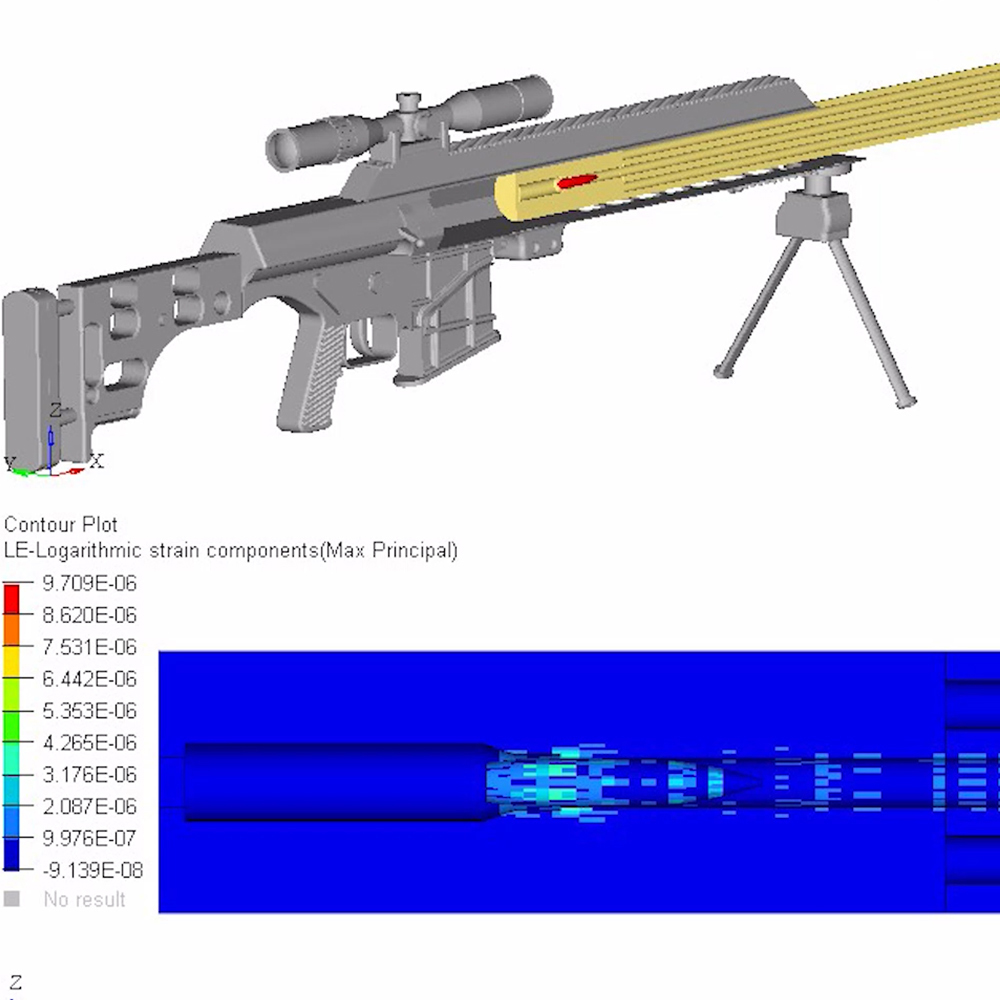
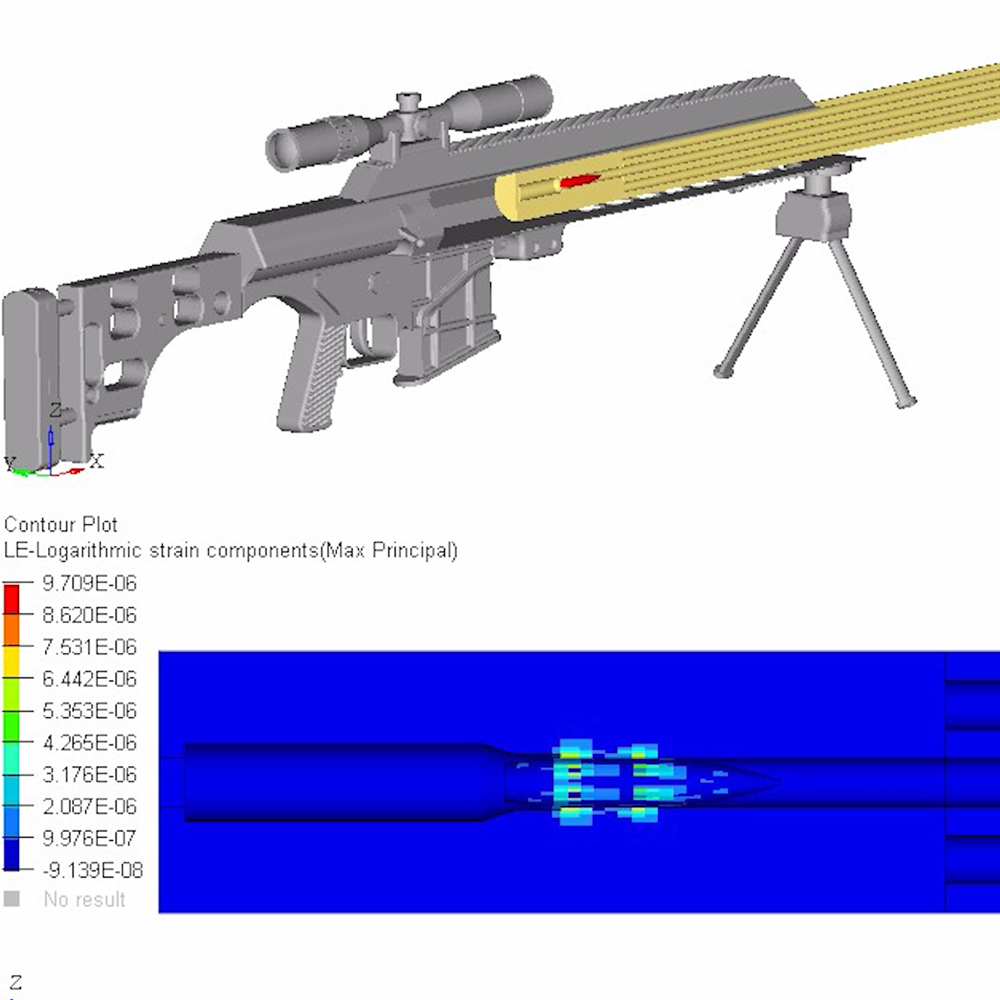
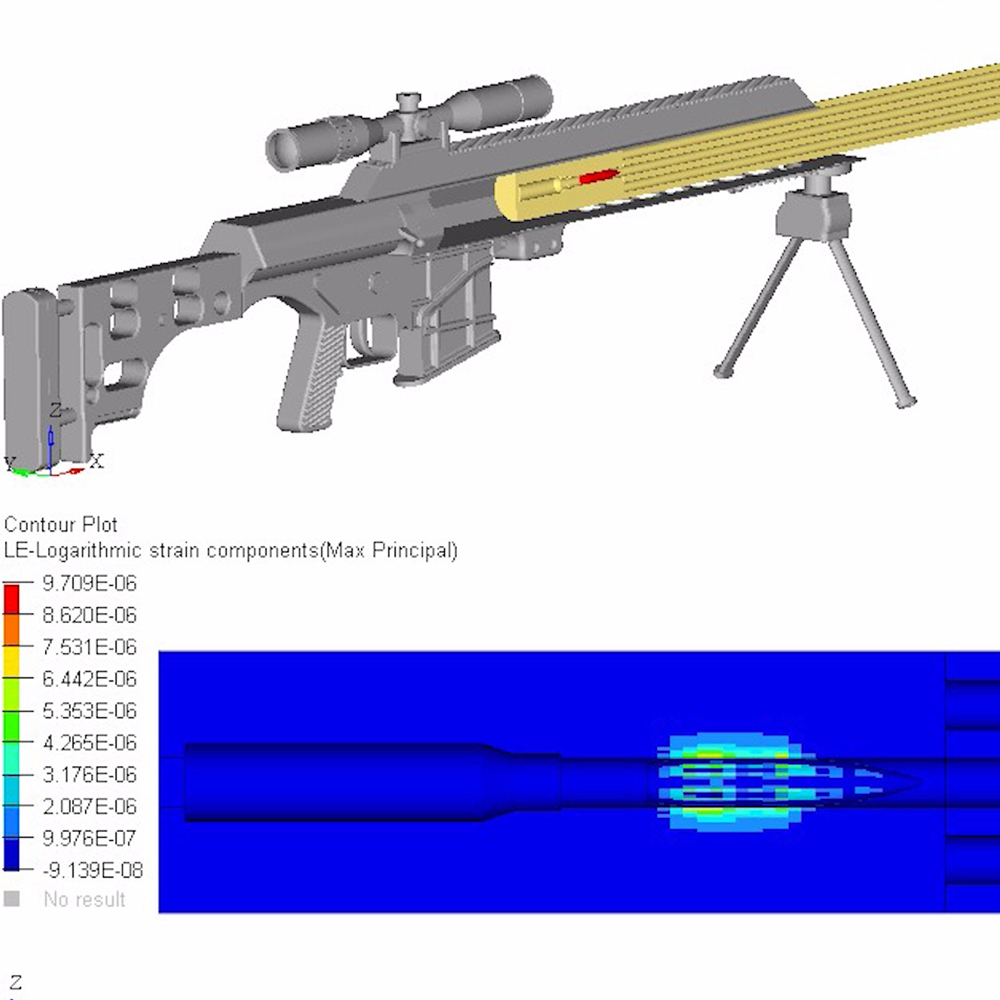
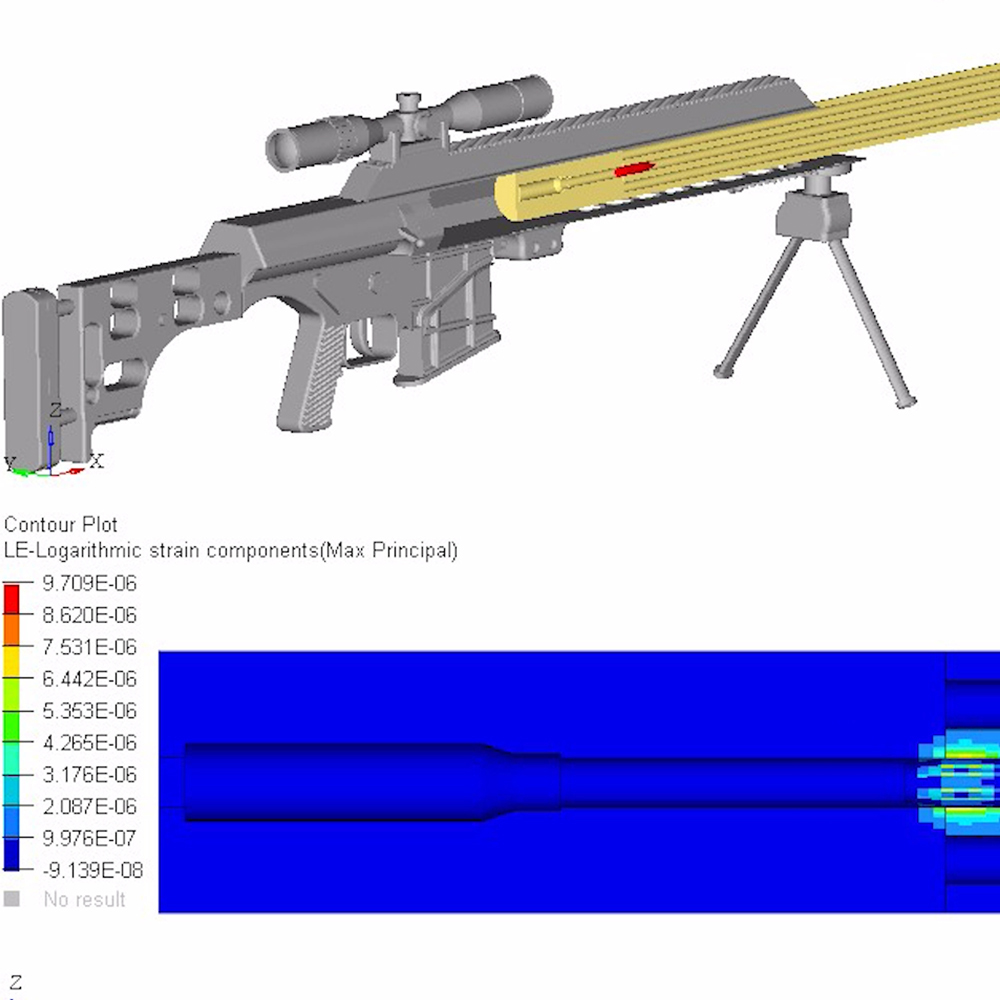
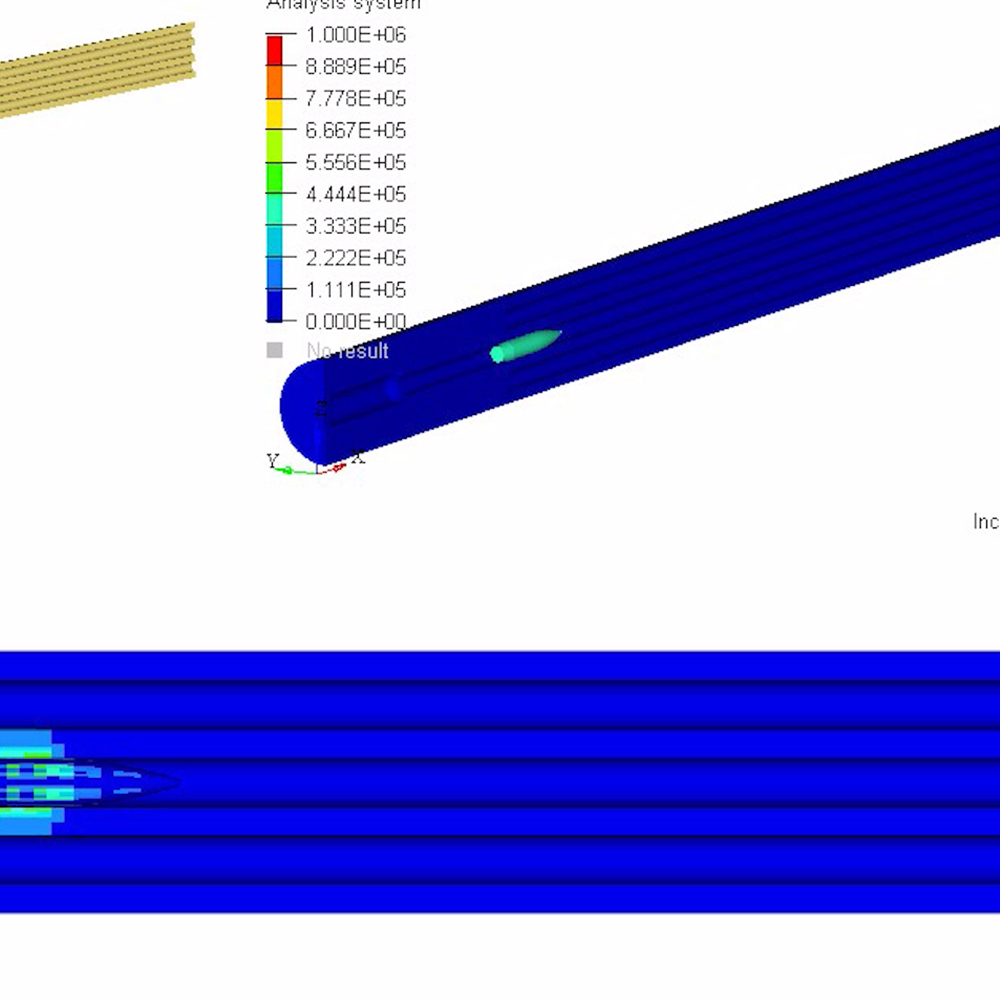
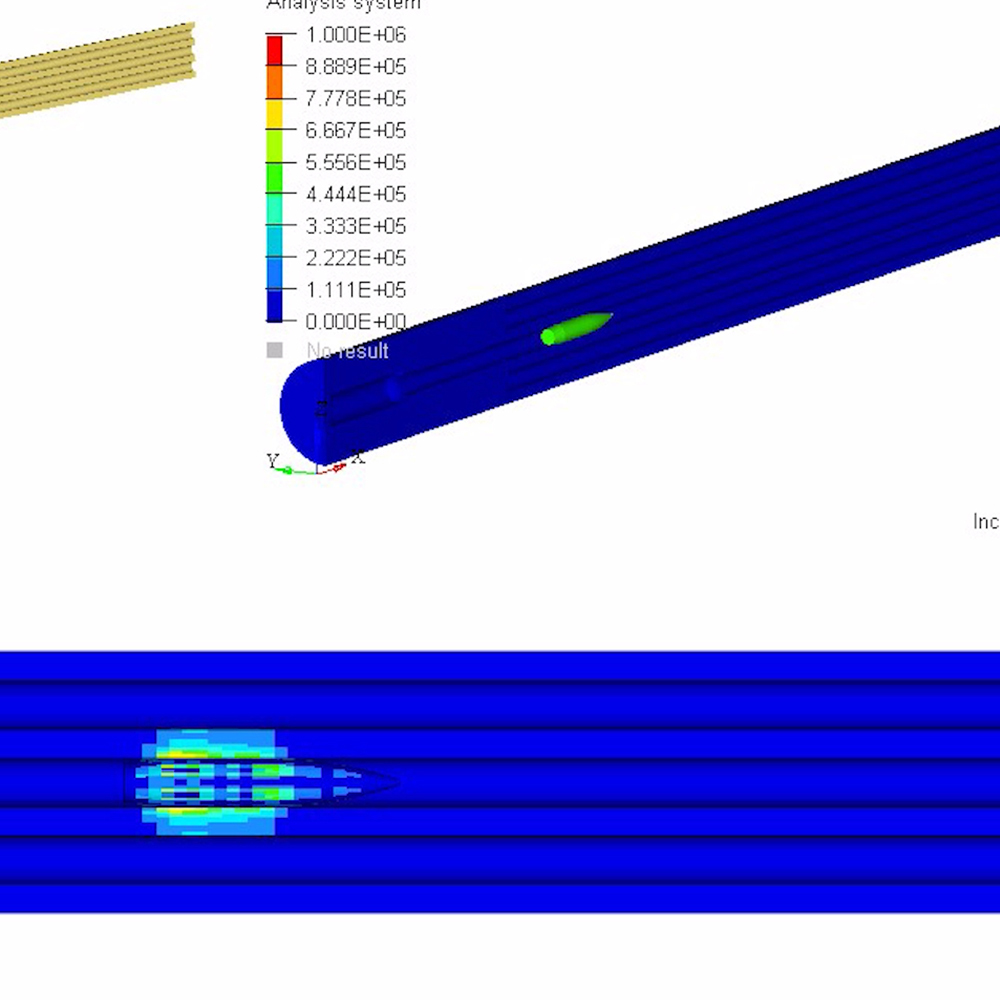
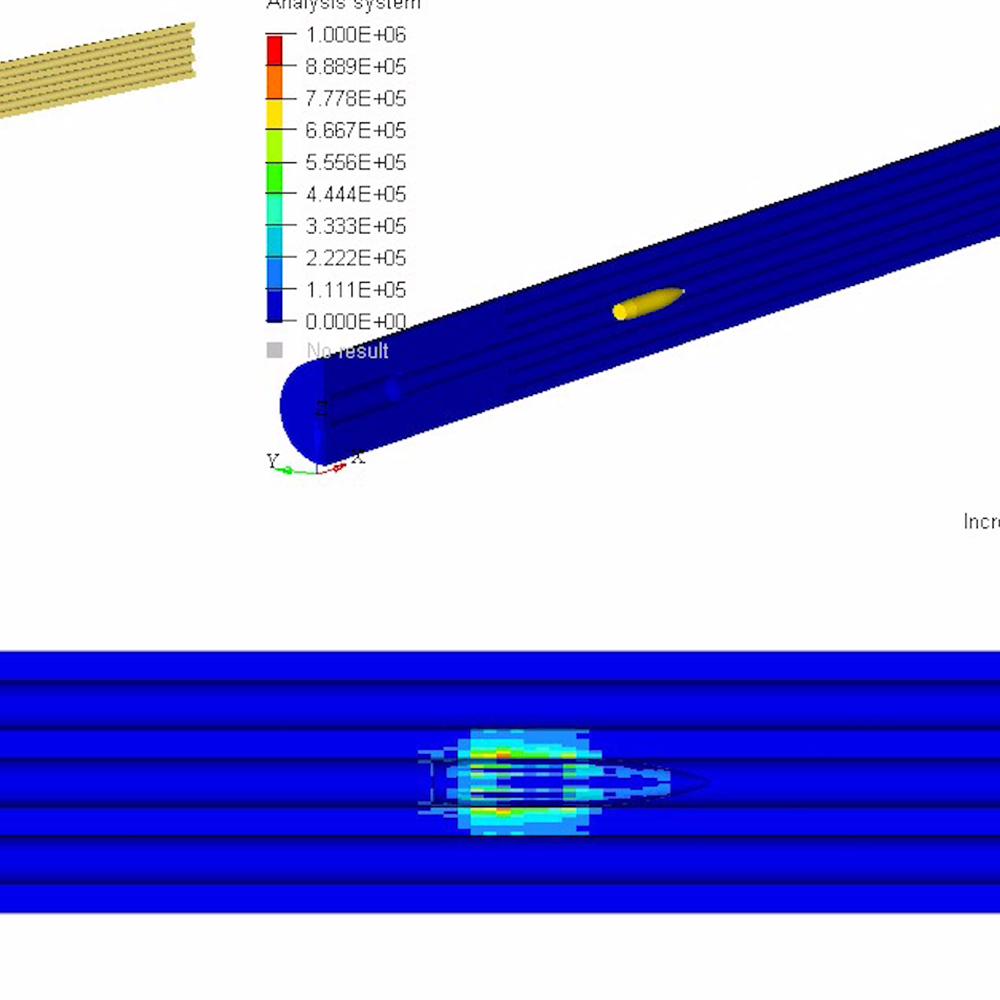
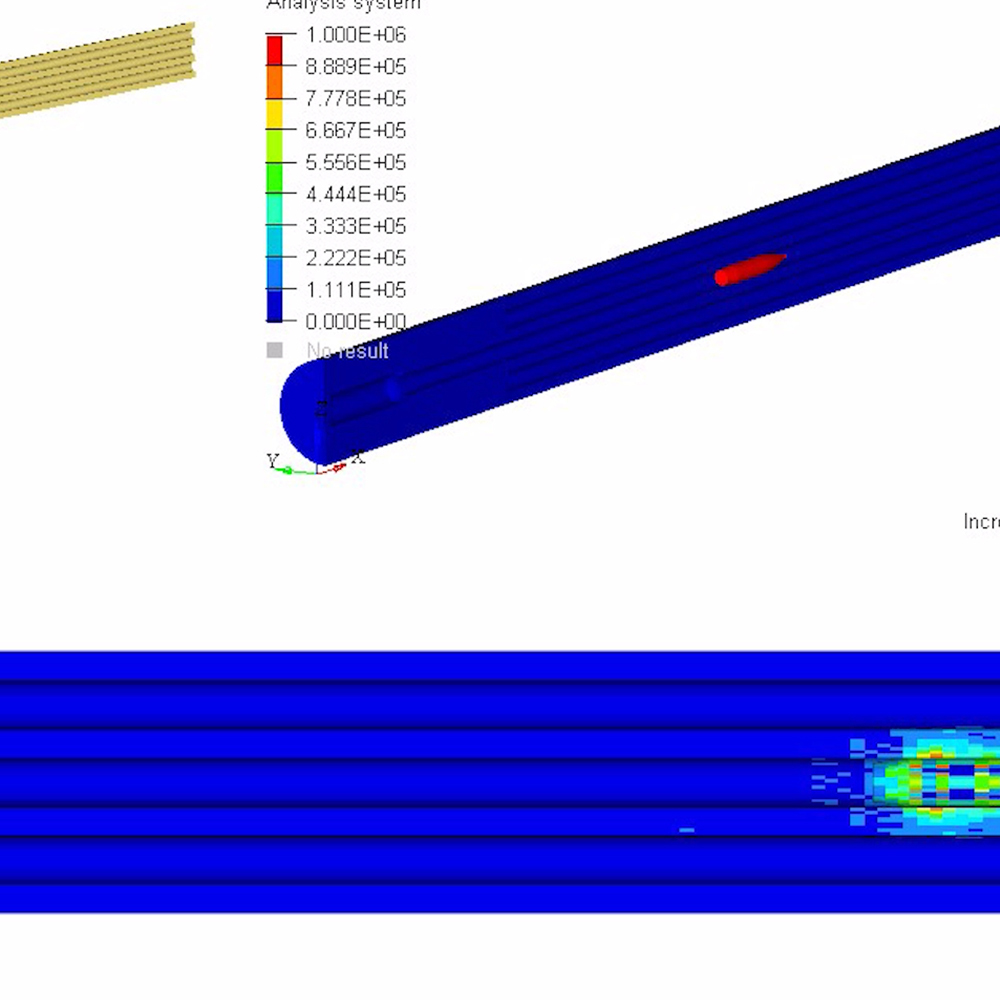
Break-in and Maintenance
Break-in
Follow the below steps for lapped barrels. Failure to do so will affect the barrel and its performance.
- Use Tubb’s break-in bullets from the TMS Kit (caliber specific).
- Load six (6) burnishing bullets from the TMS Kit at 60-75% of charge, lubing each bullet with Imperial Sizing Wax, Hornady One Shot, or equivalent, and set the seat depth so bullets do not engage the rifling.
- Thoroughly clean and remove particulates from the bore using a brush and patches; this will require significant brush-force due to adhesion forces.
- Shoot three (3) burnishing rounds.
- Thoroughly clean the barrel using a brush, patches, solvents, and detergents until you get a clean patch to prevent driving unwanted material into the barrel’s porosity.
- Shoot the remaining three (3) burnishing rounds, and proceed to thoroughly clean the barrel using a brush, patches, solvents, and detergents until you get a clean patch.
Complete. At this stage, there should be a lead into the lands and any burrs from throat operations removed.
Maintenance
• Repeat steps 1-5 as necessary for intervals will vary according to caliber, pressure, and bore conditions. Borescopes are highly recommended to guarantee a comprehensive and consistent bore cleaning.
Conventional vs. Structure
Conventional
vs.
Structure
MIL Review
“So the platform [300 Norma MRAD with +2,500 rounds] is not ideal. The weapon has issues with plastic parts and ergonomics; however, the barrel has performed better than any barrel I have used or shot against. Every person that shoots with me or against me is looking to see how to get their hands on one. With the 300 Norma, heat mirage is non-existent with your barrel and it gives me better clarity on the 1,000m plus shots. So, to answer your question, the rifle performs because of the barrel (….) I am standing very strong behind the barrel and its advantages.”

Follow-up – “I have been running my Structured Barrel for approximately 5-mo, and I’m pleased to say it has lived up to what I expected from a high-end, precision rifle barrel. When I was first introduced to the barrel, I was extremely skeptical and, like most, I had my doubts (….) That being said, I moved forward at this point with two barrels. One in my personal rifle chambered in 6mmCM and the other in a 300 Norma. I choose the 6mmCM, because I wanted a round I could compete, but also test the barrel life experience.
So far, I have completed multiple sniper matches at the highest level, and I am truly impressed. The recoil impulse as well as the heat dispersion is unparalleled. It only became apparent to me after shooting it. It’s one thing to explain to people – the different feel – and another to just put them behind the rifle for the experience. Anyone who has shot a polymer pistol and for the first time ever racked the slide on a custom 2011 will know the difference. The feel can only be explained by experience.
The barrel helped me and my sniper partner win the Army vs. Marine Grudge Match, and tie for third place overall at the Major Land Sniper Cup. This barrel has continued to play a huge role to my success and I can’t recommend them enough. During the course of fire, I have subjected the barrel to multiple high strings of 10-12 round groups with zero drift or displacement. This was confirmed on a match this past weekend, when I shot two 5-round groups into a target, then a 5-round group into a half-MOA square under the timer. Every round stayed well within the half-MOA square. Out to distance, once all the data is put in the Kestrel, it always tracks and lines up with my holds. I have no doubt in my mind when I take the shot that everything is doing what it was designed to do. This freedom gives me more time to concentrate on stage plan or whatever gear I need to prepare for the upcoming stage.
I have currently settled on a hand-load, strictly for velocity. It seems the barrel couldn’t care less what powder charge or bullet I use. It just flat out shoots them all same hole. Makes load development a thing of the past, and gives me more rounds during competition and less at a zero target under a chronograph.”
Long-range Competitor Review
“I now have 2 Structured Barrels with almost 1,000 rounds on them each. There are 3 things I believe to be particularly useful that I observed with my first barrel. They were enough to talk me into a second barrel, and my observations were still true.
Harmonics – The barrels does not seem to have any harmonic nodes. Which was the most surprising thing to me. I was able to zero the rifle and test ammo, all ammo of varying bullet weights and velocities, all grouped in the same POI. Also, I could never get a 90gr A-tip to fly right until I got your barrel.
Heat – The barrel never gets hot under normal shooting conditions. There have been a few competitions where I had to fire 20-rounds in a 2-minute engagement, and the barrel is still cool enough to grab. My partner’s barrel was untouchable for 15 minutes under the same conditions. The Structured Barrels also seem to cool faster.
Weight – They look like big, meat barrels, but they’re actually quite light for their size. I have shorter and smaller profile barrels that weight almost 2-lbs more than my Structured Barrels.

.22 NLR Competitor Review
“The first 10-rounds with the SK were one hole. One thing became very obvious to me is the ES/SD impact shows immediately, but that was it. The rifle wants put everything in the same hole. It’s like watching a video game through the scope. No recoil, no movement, nothing just deadness.
Groups at 100-yds | POA 2/10ths high:
+ 1st row CX .001RO | Avg .1675″ | Corollary Avg 1065 SD 6.7
+2nd row Midas+ no RO | Avg .268″ | Corollary Avg 1068 SD 11.4
+3rd row XACT no RO | Avg .276″ | Corollary Avg 1049 SD 8.9
+4th row Tenex no RO | Avg .272″ | Corollary 1107 SD 8.1
*RO – Run out
Δ58 FPS
Honestly, the rifle outperformed every ammo I fed it. It needs to go to Lapua and Eley for testing in their tunnels to find an ammo lot that will deliver the best SD’s. It was amazing shooting across the radar. I could tell based on where the impact went whether the velocity was high or low. I did have some ammo I was testing an Olympic runout gauge on, and the ammo performed best. And it was .001RO. I still need to shoot the .000’s I have, those will tighten up the group even more (….) Twenty years of research shows that for every .001″ of run out equates to 1/10th group size. The barrel is outstanding, and shows quickly the weak point is in the ammunition. Even though it’s Olympic ammo.
The velocity gained has been consistently 30fps, and that’s with a 4″ longer barrel than prior. ES has been cut in half and are consistently low single digits with match ammo. Shooting at a Dalt of about 7,500-ft in 95-deg weather, the Lapua SLR ammo was ~1150fps (spicy), but the groups at 200+ were incredibly tight.” – Chris Baxter
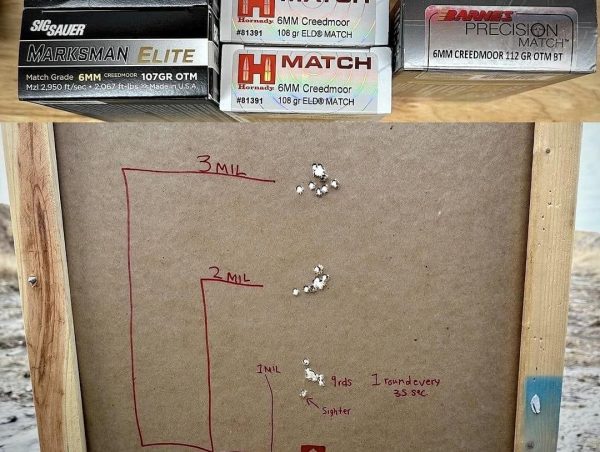
5-Round Groups from Four Different Manufacturers


PRS Competitor Review
• 3,000 Round 6mmCM Structured Barrel
• 30-round group from a Structured 6mmCM with +3,000 rounds and three (3) different factory ammos shot every 30-35s
Bottom group Sig Sauer 107gr Marksman
Middle group Hornady 108gr ELDM
Top group Barnes 112gr match burner

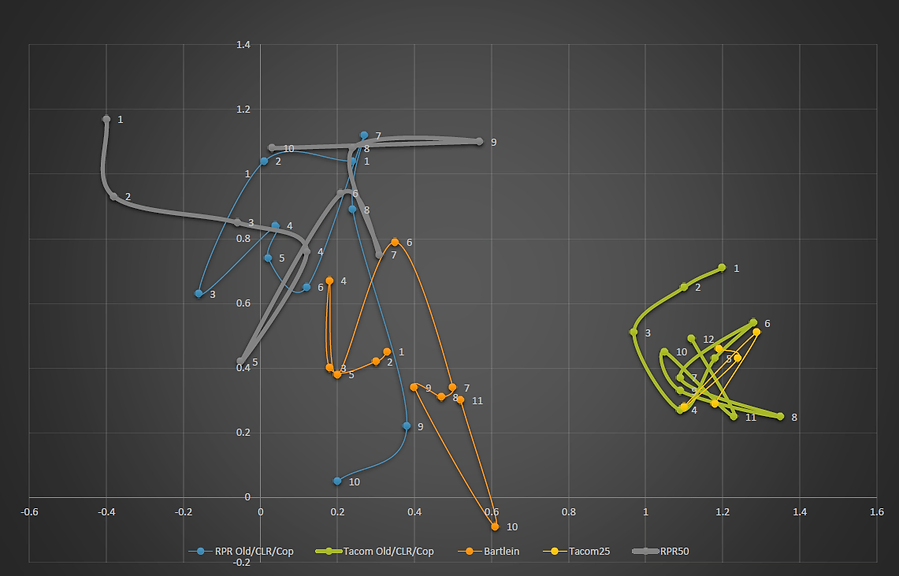
Coastal Precision
10x 5-Round Strings per Barrel Manufacturer – Total 50 Rounds
Temperature Readings of a conventional barrel
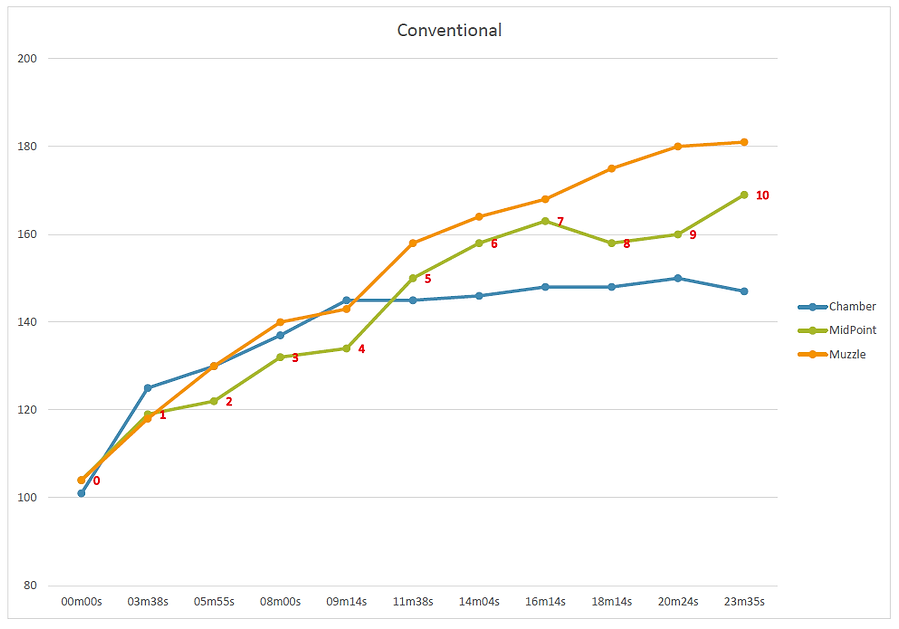
Temperature Readings of a Structured Barrel

Made in the U.S.A.
